Задать вопрос Регистрация
Помочь другим

  • Памагытее

    Не могу решить
    Докажите что при любых допустимых значениях х значение выражения не зависит от х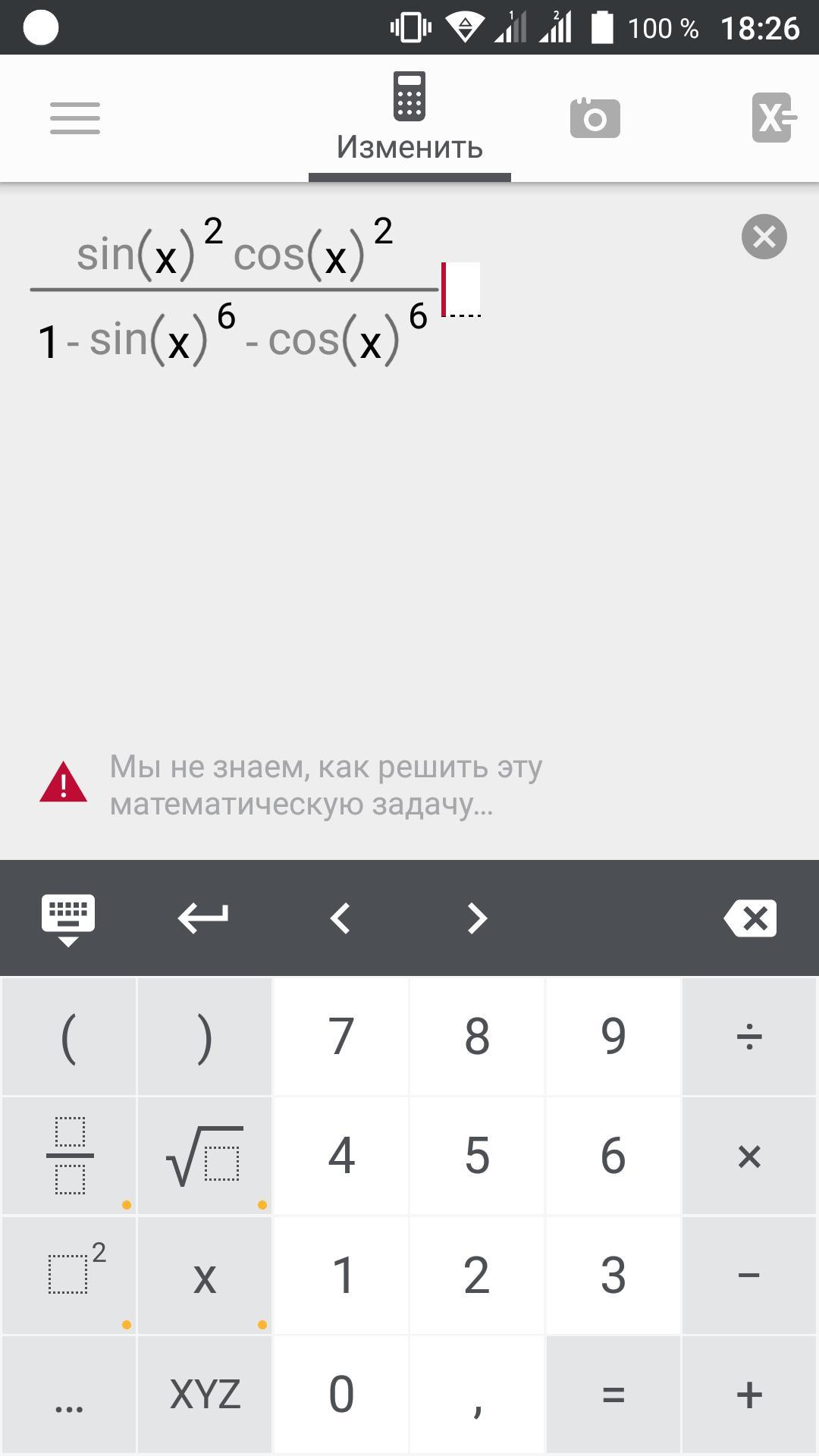

    question img

Ответы 1

  • \frac{sin^2x cos^2x}{1-sin^6x-cos^6x}=

    \frac{sin^2x cos^2x}{1-(sin^6x+cos^6x)}=

    \frac{sin^2x cos^2x}{1-[(sin^2x)^3+(cos^2x)^3]}=

    \frac{sin^2x cos^2x}{1-(sin^2x+cos^2x)(sin^4x-sin^2xcos^2x+cos^4x)}=

    \frac{sin^2x cos^2x}{1-(sin^4x-sin^2xcos^2x+cos^4x)}=

    \frac{sin^2x cos^2x}{1-sin^4x+sin^2xcos^2x-cos^4x}=

    \frac{sin^2x cos^2x}{1-(sin^2x)^2+(1-cos^2x)cos^2x-cos^4x}=

    \frac{sin^2x cos^2x}{1-(1-cos^2x)^2+cos^2x-cos^4x-cos^4x}=

    \frac{sin^2x cos^2x}{1-1+2cos^2x-cos^4x+cos^2x-2cos^4x}=

    \frac{sin^2x cos^2x}{3cos^2x-3cos^4x}=

    \frac{sin^2x cos^2x}{3cos^2x(1-cos^2x)}=

    \frac{sin^2x cos^2x}{3cos^2x sin^2x}= \frac{1}{3}

    зависит от х

    • Автор:

      kalepratt
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years