Задать вопрос Регистрация
Помочь другим

  • Нужна помощь с алгеброй
    Надо найти производную.
    Надо решить 45 и 46 номер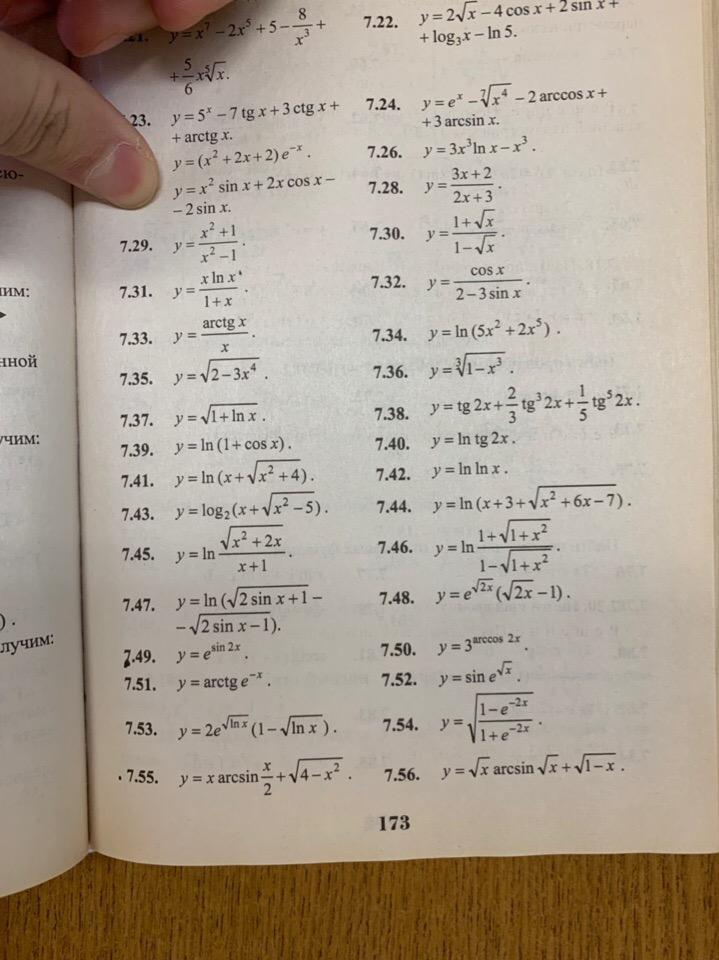

    question img

Ответы 1

  • 45.

    По свойствам логарифма:

    ln\frac{\sqrt{x^2+2x} }{x+1}=ln\sqrt{x^2+2x}-ln(x+1)=ln(x^2+2x)^{\frac{1}{2}}-ln(x+1)=\\ \\\frac{1}{2}ln(x^2+2x)-ln(x+1)\\ \\ \\y`=\frac{1}{2}(ln(x^2+2x))`-(ln(x+1))`=\frac{1}{2}\cdot\frac{(x^2+2x)`}{x^2+2x}-\frac{(x+1)`}{x+1}=\frac{1}{2}\cdot\frac{(2x+2)}{x^2+2x}-\frac{1}{x+1}=\frac{x+1}{x^2+2x}-\frac{1}{x+1}=\frac{(x+1)\cdot(x+1)-(x^2+2x)}{(x^2+2x)\cdot(x+1)}=\frac{x^2+2x+1-x^2-2x}{(x^2+2x)\cdot(x+1)}=\frac{1}{(x^2+2x)\cdot(x+1)}.

    46.

    По свойствам логарифма:

    ln\frac{1+\sqrt{1+x^2} }{1-\sqrt{1+x^2}}=ln(1+\sqrt{1+x^2})-ln(1-\sqrt{1+x^2})\\ \\ \\ y`=(ln(1+\sqrt{1+x^2}))`-(ln(1-\sqrt{1+x^2}))`=\frac{(1+\sqrt{1+x^2})`}{1+\sqrt{1+x^2}}-\frac{(1-\sqrt{1+x^2})`}{1-\sqrt{1+x^2}}=\frac{1}{1+\sqrt{1+x^2}}\cdot (0+\frac{(1+x^2)`}{2\sqrt{1+x^2}}) -\frac{1}{1-\sqrt{1+x^2}}\cdot (0-\frac{(1+x^2)`}{2\sqrt{1+x^2}} )=\\ \\ =\frac{1}{1+\sqrt{1+x^2}}\cdot (\frac{2x}{2\sqrt{1+x^2}}) -\frac{1}{1-\sqrt{1+x^2}}\cdot (-\frac{2x}{2\sqrt{1+x^2}} )=\\ \\ \frac{x}{\sqrt{1+x^2}} \cdot(\frac{1}{1+\sqrt{1+x^2}}+\frac{1}{1-\sqrt{1+x^2}})=\frac{x}{\sqrt{1+x^2}} \cdot(\frac{1-\sqrt{1+x^2}+1+\sqrt{1+x^2}}{(1+\sqrt{1+x^2})(1-\sqrt{1+x^2})}=\frac{2x}{-x^2\cdot\sqrt{1+x^2}} =-\frac{2}{x\cdot\sqrt{1+x^2}}

    • Автор:

      jamie34
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years