-
Ребята, выручайте! Без Вас никак!
Помогите разобраться в теме
Решите и подробно распишите!
Любую задачку, любое количество!
За отдельную благодарность можете Всё, хочу на ваших решениях понять тему и научиться решать эти тяжки задачи! Надеюсь на Вас!
Заранее огромное спасибо!
Помоги :)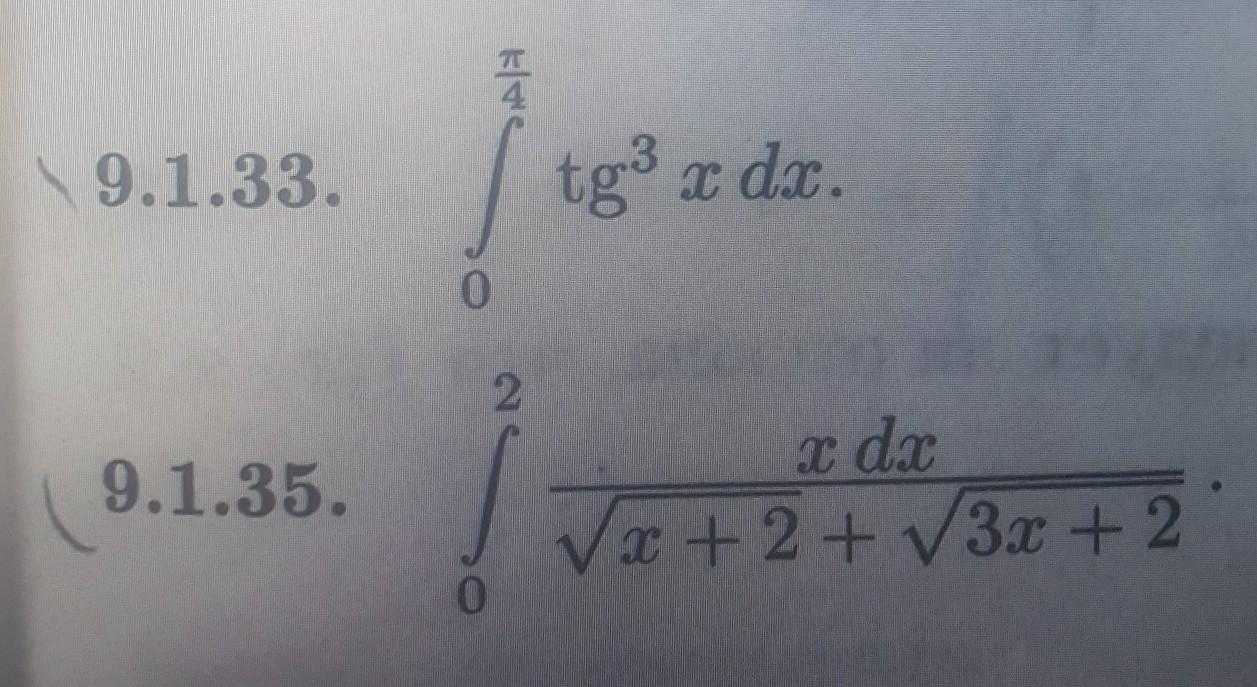
Ответы 2
-
Попыталась для вас расписать некоторые моменты подробней. Надеюсь, что-то станет понятней в этой теме.

-
Автор:
románfro0 - 6 лет назад
-
0
-
-

-
Автор:
ilianasesm - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Что было предсказанно Ассоль.Как стали относится к ней в Коперне после этого????
-
Предмет:
Литература -
Автор:
rowland - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
найдите архимедову силу,действующую на батискаф обьемом 7 м^3 . Погруженый в морскую воду .
Пожалуйста -
Ребята, выручайте! Без Вас никак!
Помогите разобраться в теме
Решите и подробно распишите!
Любую задачку, любое количество!
За отдельную благодарность можете Всё, хочу на ваших решениях понять тему и научиться решать эти тяжки задачи! Надеюсь на Вас!
Заранее огромное спасибо!
Помоги :) -
Что такое МБД ?????
Срочно !!!
How much to ban the user?
1 hour
1 day
100 years
