Задать вопрос Регистрация
Помочь другим

  • Пожалуйста спасите, помогите, выручайте
    Помогите разобраться в теме
    Решите и подробно распишите!
    Любую задачку, любое количество!
    За отдельную благодарность можете Всё, хочу на ваших решениях понять тему и научиться решать эти тяжки задачи! Надеюсь на Вас!
    Заранее огромное спасибо!
    Помоги :)​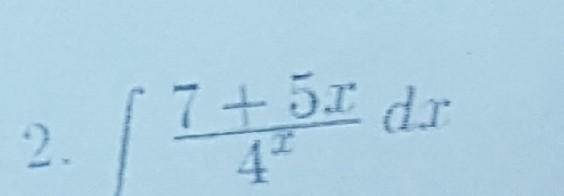

    question img

Ответы 2

  • спасибо

  • \int \frac{7+5x}{4^{x}}\, dx=\int \Big (\frac{7}{4^{x}}+\frac{5x}{4^{x}}\Big )dx=7\int 4^{-x}\, dx+5\int x\cdot 4^{-x}\, dx=Q\\\\\\\star \; \int 4^{-x}\, dx=[\; t=-x\; ,\; dt=-dx\; ]=-\int 4^{t}dt=-\frac{4^{t}}{ln4}+C=-\frac{4^{-x}}{ln4}+C\; ;\\\\\\\star \; \int x\cdot 4^{-x}\, dx=[\; u=x,\; du=dx,\; dv=4^{-x}dx,\; v=\int 4^{-x}\, dx=-\frac{4^{-x}}{ln4}\; ]=\\\\=uv-\int v\, du=-\frac{x\cdot 4^{-x}}{ln4}+\frac{1}{ln4} \int \, 4^{-x}\, dx=-\frac{x\cdot 4^{-x}}{ln4}+\frac{1}{ln^24}\cdot 4^{-x}+C=

    =\frac{4^{-x}}{ln4}\cdot (\frac{1}{ln4}-x)+C\; ;\\\\\\Q=-7\cdot \frac{4^{-x}}{ln4}+5\cdot \frac{4^{-x}}{ln4}\cdot \Big (\frac{1}{ln4}-x\Big )=\frac{4^{-x}}{ln4}\cdot \Big (\frac{5}{ln4}-5x-7\Big )

    • Автор:

      sophie28
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years