-
Решить интеграл методом универсальной тригонометрической подстановки ( Номер 9 )
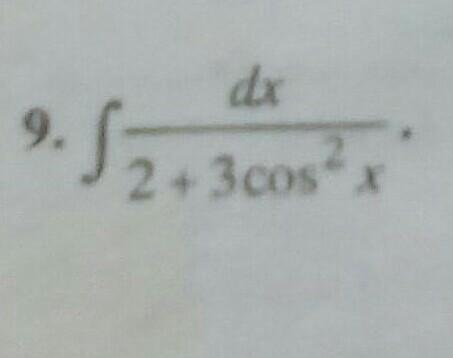
Ответы 1
-
2+3cos^2x=2+3/2(1+cos2x)
dx/(2+3cos^2x)=2dx/(7+3cos2x)
tgx=t cos2x=(1-t^2)/(1+t^2)
dx=2/(1+t^2)
(4/(1+t^2))/(7+3(1-t^2)/(1+t^2))=2/(5+2t^2)
2/5(1+((√2/5)t)^2
интеграл = 2/5*arctg(sqrt(0,4)t)*sqrt(5/2)=sqrt(0.4)arctg(sqrt(0.4)t)
обратная замена
ответ sqrt(2/5)*arctg(sqrt(2/5)tgx)+C
-
Автор:
coltonomjj - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Плата за телефон составляет 350 рублей в месяц. В следующем году она увеличится на 14%. Сколько рублей придется платить ежемесячно за телкфон в следующем году.
-
Предмет:
Математика -
Автор:
terrellrivas - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- { x2+3x-4=0 > x2+10x+24=0
-
Помогите решить уравнение
2 14/23+x=5 13/23-
Предмет:
Математика -
Автор:
antonyponce - 6 лет назад
-
Ответов:
3 -
Смотреть
-
- как доказать равенство уровней поверхности однородной жидкости в открытых сообщающихся сосудах
How much to ban the user?
1 hour
1 day
100 years
