-
Пожалуйста, помогите!!! решить пределы применив правило Лопиталя 4 и 7 номера)
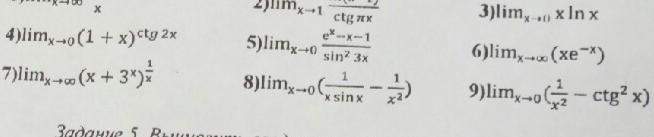
Ответы 2
Еще вопросы
- Привести примеры обращения композиторов к образцам духовной музыки при создании музыкальных произведений.Пожалуйста побольше
-
Назовите функцию слепого пятна.
-
Предмет:
Биология -
Автор:
nikolasgill - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
укажите части женской половой системы обозначенной на рисунке 15 цифрами 1-5
-
Предмет:
Биология -
Автор:
irelandvalentine - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
6 класс немецкий язык, найти слова, даю 35 баллов
Пожалуйста, очень срочно
-
Предмет:
Немецкий язык -
Автор:
cristóbalwoods - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
