-
помогите, пожалуйста, прошу! желательно через плоскость aox (но можно и любым другим способом)
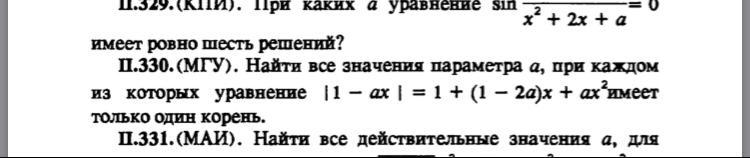
Ответы 1
-
Раскрываем модуль по определению:
1-ax ≥0 ⇒ ax ≤ 1
Уравнение принимает вид:
1-ax=1+(1-2a)x+ax^2
ax^2+(1-a)x=0
На плоскости хOа
ax ≤ 1 ⇒ a≤1/x- область между двумя ветвями гиперболы a=1/x
ax^2+(1-a)x=0 ⇒ ax^2+x-ax=0 ⇒ a·(x^2-x)=-x ⇒ a=-1/(x-1)
Уравнение имеет решение в области при
a∈(-∞;0)U(0;2]
см. рис.1
1-ax < 0 ⇒ ax > 1
Уравнение принимает вид:
-1+ax=1+(1-2a)x+ax^2
ax^2+(1-3a)x+2=0
На плоскости хOа
ax > 1 ⇒ a> 1/x- внешняя часть гиперболы a = 1/x
ax^2+(1-3a)x+2=0 ⇒ ax^2+x-3ax+2=0 ⇒ a·(x^2-3x)=-x-2 ⇒ a=-(х+2)/(x^2-3x)
Исследуем функцию с помощью производной и строим график.
Уравнение имеет решение в области при
a∈(-∞;0)U [2;+∞)
см. рис. 2
Ответ. a∈(0;2) U(2;+∞)

-
Автор:
víctorcarrillo - 6 лет назад
-
0
-
-
Добавить свой ответ
-
(0,01812 : 0,003 * 0,5) : (0,2718 : 1,8 * 5)
-
Предмет:
Математика -
Автор:
ferrera8ii - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Небольшой пересказ о спасении Пятницы из произведение ,,Приключения Рабинзона Крузо" от лица Пятницы Помогите срочно даю 34 баллов!!!!
-
Предмет:
Литература -
Автор:
jack25 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Пожалуйста, помогите! Как можно сделать этот рисунок в paint? Особенно окна не понимаю.
-
Предмет:
Информатика -
Автор:
ashtynriddle - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
5 Раскрой скобки и напиши предложения в будущем времени:
1. Ton ami t`(inviter) a cette soiree?
2. Qu`est-ce que tu (acheter) a ta cousine pour son anniversaire?
3. Ma vie au 21 siecle (etre) belle.
4. J`(avoir) une superbe voiture .
5. Le dimanche nous (manger) ensemble.-
Предмет:
Французский язык -
Автор:
ciarawatts - 6 лет назад
-
Ответов:
2 -
Смотреть
-
