-
Решите логарифмическое неравенство
(10 класс; уровень сложности: средний)
Смотрите фотографию (Задание 2)
Оформить письменно!
x^lg(x)<=100x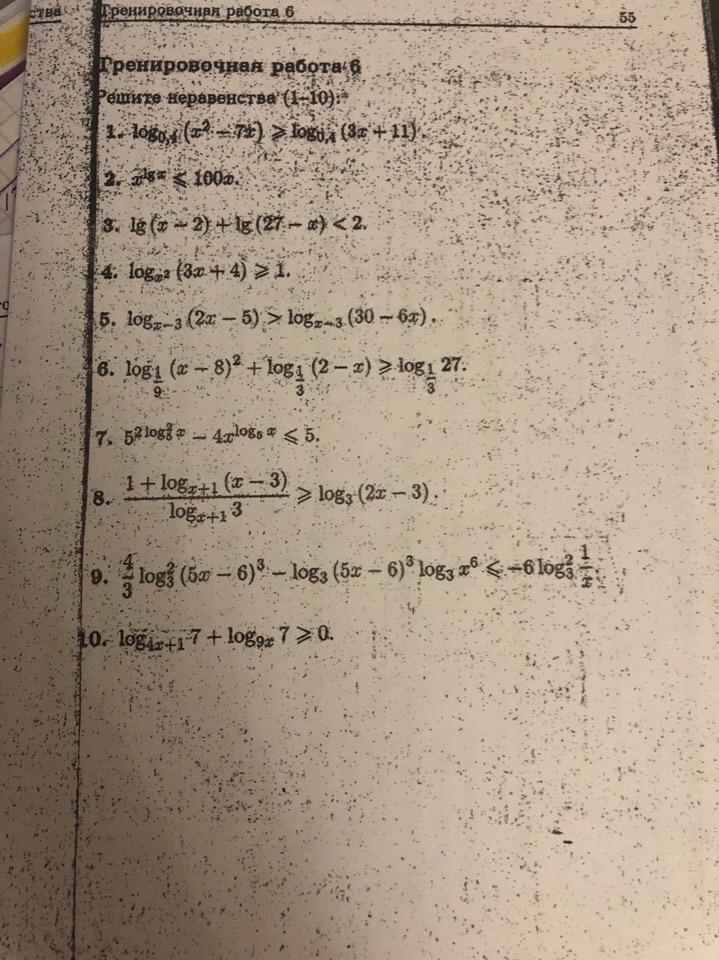
Ответы 2
-
Извините, а вы не знаете, как решить 7 и 10 задание?Я просто задавал вопрос по решению этих неравенств, так никто и не сумел решитьМогу отправить ссылку вам на эти заданияТам я даю по 30; 45 баллов...
-
Автор:
chevyvargas - 6 лет назад
-
0
-
-
ОДЗ: x > 0
следовательно, обе части неравенства--это положительные числа)
можно прологарифмировать обе части неравенства по основанию 10:
lg(x) * lg(x) ≤ lg(100) + lg(x)
заменой t=lg(x) неравенство сведется к квадратичному...
t² - t - 2 ≤ 0 по т.Виета корни t₁=2 и t₂=-1
и решение "между корнями" (парабола, ветви вверх...)
-1 ≤ lg(x) ≤ 2
lg(0.1) ≤ lg(x) ≤ lg(100) основание логарифма 10>1 ⇒ знаки не меняются...
0.1 ≤ x ≤ 100
-
Автор:
wayne - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Теоретическое исследование ценностей и оценок составляет содержание _______ функции философии.
-
Предмет:
Другие предметы -
Автор:
angelique - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
ПОЧЕМУ человек на половину состоит из воды? ∠ °ω° √
-
Предмет:
Окружающий мир -
Автор:
devanpvpc - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Пословицы, загадки, поговорки с определительными местоимениями. В сумме должно быть минимум 15.
-
Предмет:
Русский язык -
Автор:
micheall6n3 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
1.)4.8:(7/16+(3/4)в квадрате)
2.) упростить и найти значение m+2/7m+4/9m-2/7 при m=9/13 m=18
3.)4/5(8-2x)=0,8(x-1)
помогите пжж
-
Предмет:
Математика -
Автор:
brynleeponce - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
