-
Помогите пожалуйста! Любой как сможете! Номер 527! Упростите выражение! Какой сможете! Любой!
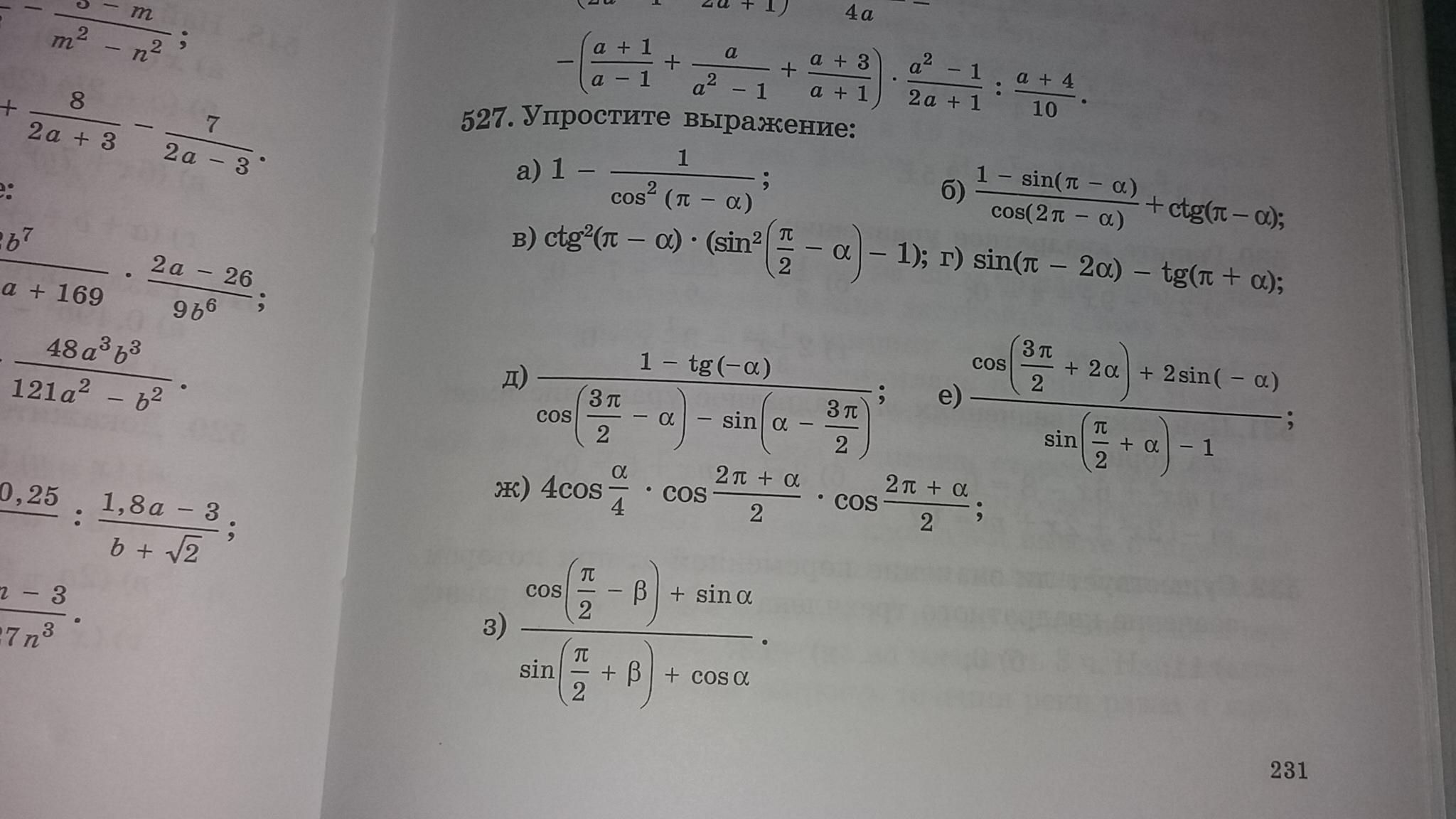
Ответы 2
Еще вопросы
-
какой храм в Москве посвящен героям войны 1812 года
-
Предмет:
Окружающий мир -
Автор:
lunavlqo - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Помогите ещё раз с математикой,только вот с этим номером.
-
Предмет:
Математика -
Автор:
harleyatkinson - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
Если честно то я 4 класс. Помогите с задачей! На выпускном были ученики и они решили обменяться фотографиями которых было 20. Сколько учеников было на выпускном?
-
Предмет:
Математика -
Автор:
slyyhax - 6 лет назад
-
Ответов:
8 -
Смотреть
-
-
К представителем Европеойдной рассы относятся
-
Предмет:
География -
Автор:
rapunzel6p67 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
