-
Помогите решить, буду очень благодарна. Тема частные производные.
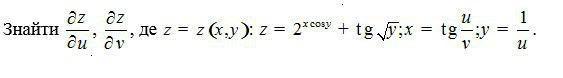
-
Предмет:
Алгебра -
Автор:
concepciónivai - 6 лет назад
-
Ответы 2
-
большое спасибо
-
Автор:
oliviamiller - 6 лет назад
-
0
-
-
-
Автор:
johnny7odg - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
СРОЧНО!!! ДАЮ 24 БАЛА!!!!!!!! Опишіть дослід Торічеллі
-
Предмет:
Физика -
Автор:
rightyv5wq - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите
Доброе утро. удачного дня...
Продолжение чтобы была рифма-
Предмет:
Литература -
Автор:
texcvvi - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Производная функции у(х) = с равна чему???(0,1,c,cx,x) -в скобках варианты ответов,всем ставлю спасибо
-
Предмет:
Математика -
Автор:
arjun - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите решить четвёртое упражнение Казах тылы 5 класс
Я не понял -
Предмет:
Қазақ тiлi -
Автор:
skylaryq6v - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
