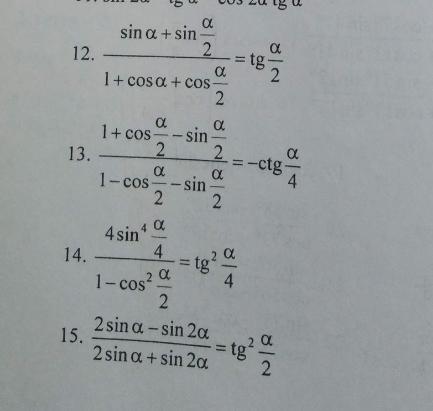Ответы 1
-
12.
13.
14.
15.
-
Автор:
charles80 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Каким образом Петр 3 подготовил восшествие на престол Екатерины 2
-
Рассчитайте относительные молекулярные массы веществ -
H2CO3 и Al2(SO4)3.
- длина взрослого растения сфагнового мха 25 см, ежегодный прирост 3 см. Чему будет равна длина сфагнума через 8 лет
-
Конспект по темі:Середнє арифметичне
-
Предмет:
Математика -
Автор:
jordin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years