Тригонометрическое УРАВНЕНИЕ : 4cos^2x-sinx*cosx-1=0 Решите пожалуйста подробно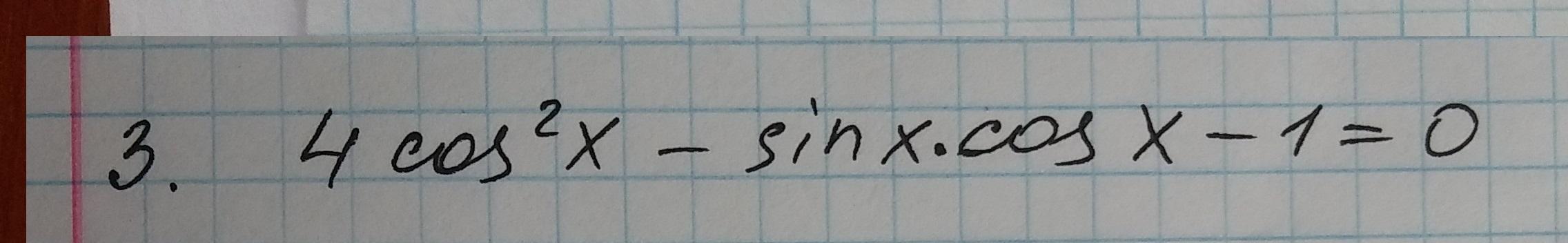 - Знания.site

Тригонометрическое УРАВНЕНИЕ : 4cos^2x-sinx*cosx-1=0
Решите пожалуйста подробно
- Предмет:
  Алгебра
- Автор:
  joshpace
- 5 лет назад

Ответы 4

А что такое tan ? Это тангенс ?
- Автор:
  foxy ladyap1z
- 5 лет назад
- 0
да
- Автор:
  chico11
- 5 лет назад
- 0
ок
- Автор:
  miss piggy
- 5 лет назад
- 0
$4\cos^2{x}-\sin{x}*\cos{x}-1=0\\4\cos^2{x}-\sin{x}*\cos{x}-\sin^2{x}-\cos^2{x}=0\\3\cos^2{x}-\sin{x}*\cos{x}-\sin^2{x}=0$
Если cos²x=0, то выражение написанное сверху будет представлять из себя следующее -sin²x=0, то есть sinx и cosx=0, а значит и их сумма равна 0, но по основному тригонометрическому тождеству мы знаем, что сумма квадратов косинуса и синуса всегда равняется 0 из чего можно сделать вывод, что cos²x≠0, тогда мы можем делить на него не потеряв корни.
$3\cos^2{x}-\sin{x}*\cos{x}-\sin^2{x}=0|:\cos^2{x}\\\left \{ {{3-\tan{x}-\tan^2{x}=0} \atop {\cos^2{x}eq 0}} ight. \\\tan{x}=a\\-a^2-a+3=0;D=1+12=13\\a=\frac{1б\sqrt{13} }{-2}$
cosx≠0 и tanx=... всегда будут пересекаться, потому что cosx≠0 это условие существования тангенса, когда cosx=0, тангенс не определён.
Ответ: $x=\arctan{\frac{-1б\sqrt{13} }{2}}+\pi n,n\in Z.$
- Автор:
  wheeler
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

How much to ban the user?

1 hour 1 day 100 years