Задать вопрос Регистрация
Помочь другим

  • Решить предел при помощи алгебраических преобразований (не правило Лопиталя)

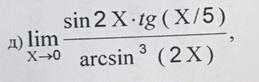
    question img

Ответы 1

  • Ответ: ∞.

    Объяснение:

    Воспользуемся эквивалентностью функций:

    \sin 2x\sim 2x,~~ {m tg}\frac{x}{5}\sim \frac{x}{5},~~~~ \arcsin 2x\sim 2x,~~~ as~~~ x\to 0

    \displaystyle \lim_{x \to 0}\frac{\sin2x{m tg}\frac{x}{5}}{\arcsin^32x}=\lim_{x \to 0}\frac{2x*\frac{x}{5}}{(2x)^3}=\frac{1}{20}\lim_{x \to 0} \frac{1}{x}=\infty

    • Автор:

      lauran3oq
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years