Решите задание на фото.Алгебра, задание с параметром.Решите срочно,97 баллов.

Решите задание на фото.Алгебра, задание с параметром.Решите срочно,97 баллов.
- Предмет:
  Алгебра
- Автор:
  josec9mc
- 5 лет назад

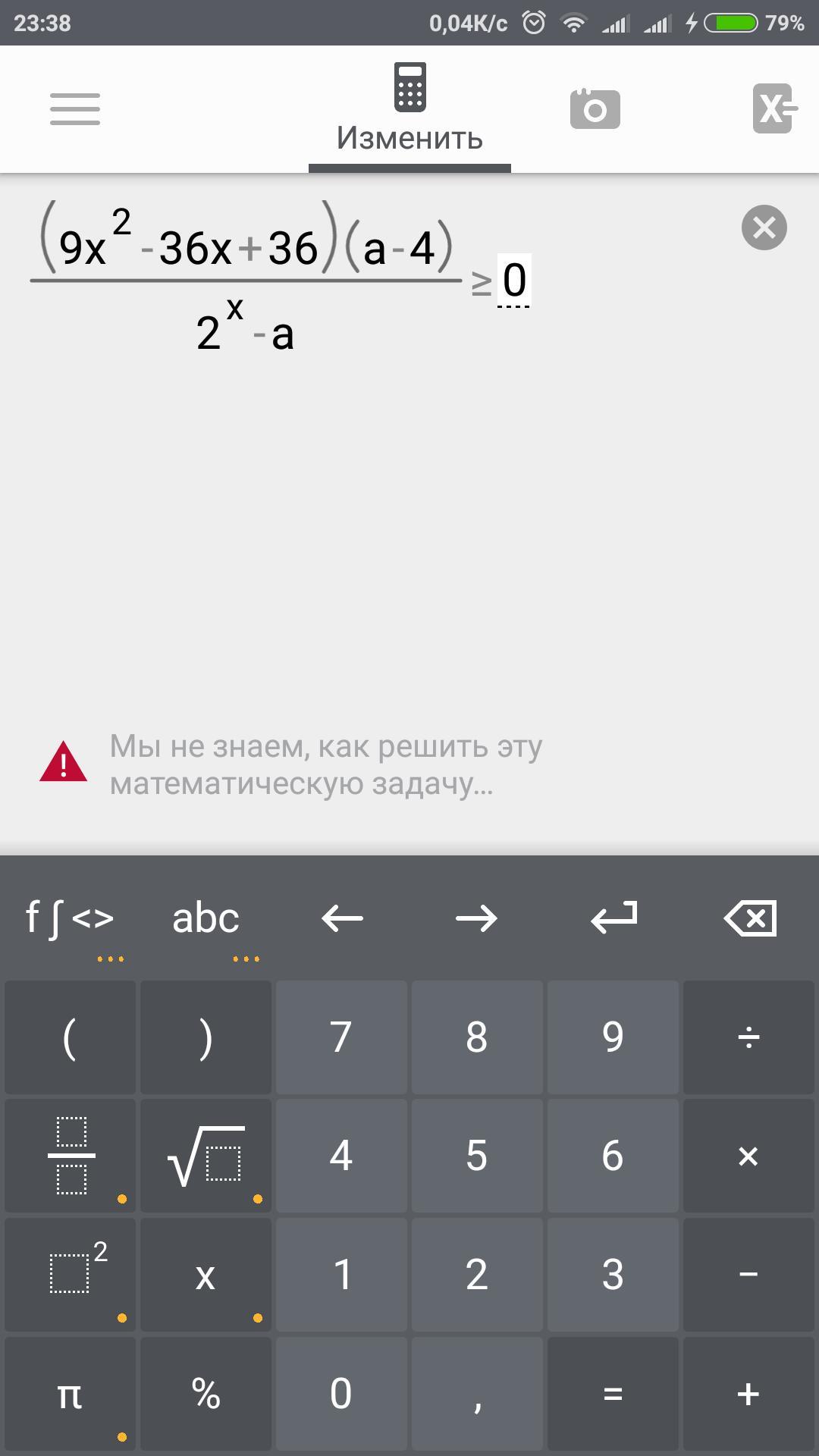
Ответы 1

$\frac{(3x-6)^2(a-4)}{2^x-a}\ge 0.$ ОДЗ: $2^xot= a.$
1-й случай. x=2 - обращает дробь в ноль. Поэтому x=2 является решением при любом a, за исключением случая, когда $a=2^2=4,$ поскольку в этом случае знаменатель обращается в ноль.
2-й случай. $xot=2\Rightarrow (3x-6)^2>0\Rightarrow$ этот множитель можно отбросить. Получаем
$\frac{a-4}{2^x-a}\ge 0.$
Если $a\le 0,$ числитель отрицателен, знаменатель положителен, поэтому дробь отрицательна, и решений нет.
Если $a\in (0;4),$ числитель отрицателен, поэтому для положительности дроби нужно, чтобы знаменатель был отрицателен, $2^x-a<0;\ x<\log_2 a$ .
Если a=4, дробь равна нулю; x - любой (естественно, за исключением x=2 - об этом мы говорили раньше).
Если a>4, числитель положителен, поэтому для положительности дроби нужно, чтобы знаменатель был положителен, $2^x>a;\ x>\log_2 a$
Ответ: $a\le 0\Rightarrow x=2$
$a\in (0;4)\Rightarrow x\in (-\infty; \log_2 a)\cup \{2\}$
$a=4\Rightarrow x\in (-\infty;2)\cup (2;+\infty)$
$a>4\Rightarrow x\in \{2\}\cup (\log_2 a;+\infty)$
- Автор:
  clinton1wyu
- 5 лет назад
- 0
Добавить свой ответ