Нужно найти х и у из тождества, но у меня получается уравнение с тремя неизвестными

Нужно найти х и у из тождества, но у меня получается уравнение с тремя неизвестными
- Предмет:
  Алгебра
- Автор:
  purdynoss
- 5 лет назад

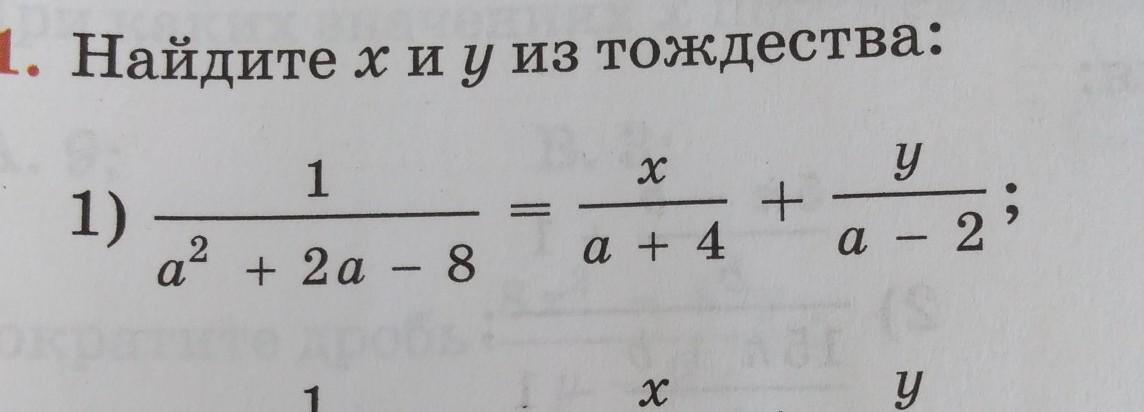
Ответы 1

Смысл задачи: найти такие x и y, чтобы это равенство было справедливо при всех допустимых значений a (то есть для всех, кроме -4 и 2).
1-й способ.
$\frac{1}{a^2+2a-8}=\frac{1}{(a+4)(a-2)}=\frac{1}{6}\frac{(a+4)-(a-2)}{(a+4)(a-2)}=\frac{1}{6}\left(\frac{1}{a-2}-\frac{1}{a+4}ight)=\frac{-\frac{1}{6}}{a+4}+\frac{\frac{1}{6}}{a-2}$
2-й способ.
Запишем равенство в виде $\frac{1}{(a+4)(a-2)}=\frac{x(a-2)+y(a+4)}{(a+4)(a-2)}.$
знаменатели в левой и правой части совпадают, поэтому совпадают числители:
x(a-2)+y(a+4)=1.
Дальше у нас есть две возможности рассуждения. При первой подставляем в это равенство a=2, находя при этом y=1/6, а затем подставляем a=-4, находя x=-1/6.
При втором способе рассуждения запишем равенство в виде
(x+y)a+(-2x+4y)=1. Поскольку это равенство должно быть справедливо при всех значениях a, получаем систему $\left \{ {{x+y=0} \atop {-2x+4y=1}} ight. ,$ решив которую, получим те же значения x и y.
Ответ: $x=-\frac{1}{6};\ y=\frac{1}{6}$
- Автор:
  caesar86
- 5 лет назад
- 0
Добавить свой ответ