Задать вопрос Регистрация
Помочь другим

  • Вычислите несобственные интегралы или установить их расходимость
    см. фото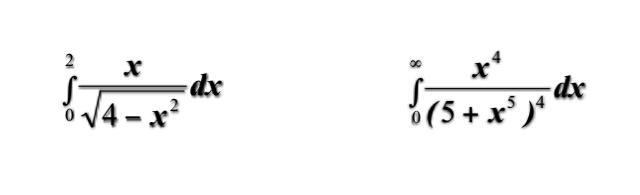

    question img

Ответы 6

  • И во втором, там разве не b->oo?

    • Автор:

      cutieg6wo
    • 5 лет назад
    • 0
  • оба сходятся... какой буквой обозначить предел интегрирования неважно, хотите, пишите "b"

    • Автор:

      zaneo5wj
    • 5 лет назад
    • 0
  • Спасибо большое!

    • Автор:

      chase131
    • 5 лет назад
    • 0
  • Под а, где замена, там разве не dt=-2xdx?

    • Автор:

      aydinlb2b
    • 5 лет назад
    • 0
  • я в скобках написала как через замену вычислить неопред. интеграл (чтоб было понятно), но далее писала через подведение под знак дифференциала, чтобы не считать пределы интегрирования новой переменной

  • 1)\; \; \int\limits^2_0\, \frac{x}{\sqrt{4-x^2}}\, dx=[\; t=4-x^2\; ,\; dt=-2t\, dt\; ,\; \int \frac{dt}{\sqrt{t}}=2\sqrt{t}+C\; ]=\\\\=-\frac{1}{2}\int\limits^2_0\, \frac{d(4-x^2)}{\sqrt{4-x^2}}\, dx=-\frac{1}{2}\cdot \lim\limits _{\varepsilon \to 0}\, 2\sqrt{4-x^2}\Big |_0^{2-\varepsilon }=-(\sqrt{0}-\sqrt4)=2\\\\sxoditsya

    2)\; \; \int\limits\, \frac{x^4}{(5+x^5)^4} \, dx=[\; t=5+x^5\; ,\; dt=5x^4\, dx\; ]=\frac{1}{5}\int \frac{dt}{t^4}=\\\\=\frac{1}{5}\cdot \frac{t^{-3}}{-3}+C=-\frac{1}{15t^3}+C=-\frac{1}{15(5+x^5)^3}\; ;\\\\\int\limits_0^{+\infty }\, \frac{x^4}{(5+x^5)^4}\, dx=\lim\limits _{A \to +\infty}\int\limits_0^{A}\, \frac{x^4}{(5+x^5)}\, dx=\lim\limits _{A \to +\infty}(-\frac{1}{15(5+x^5)^3})\Big |_0^{A}=\\\\=-\frac{1}{15}\cdot \lim\limits _{A \to +\infty}(\frac{1}{(5+A^5)^3}-\frac{1}{5^3})=-\frac{1}{15}\cdot (0-\frac{1}{125})=\frac{1}{15\cdot 125}=\frac{1}{1875}\\\\sxoditsya

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years