-
Помогите решить примеры по математике.
Тема: Решение тригонометрических уравнений или тригонометрические уравнения
Очень срочно!
Могу точнее объяснить вопрос.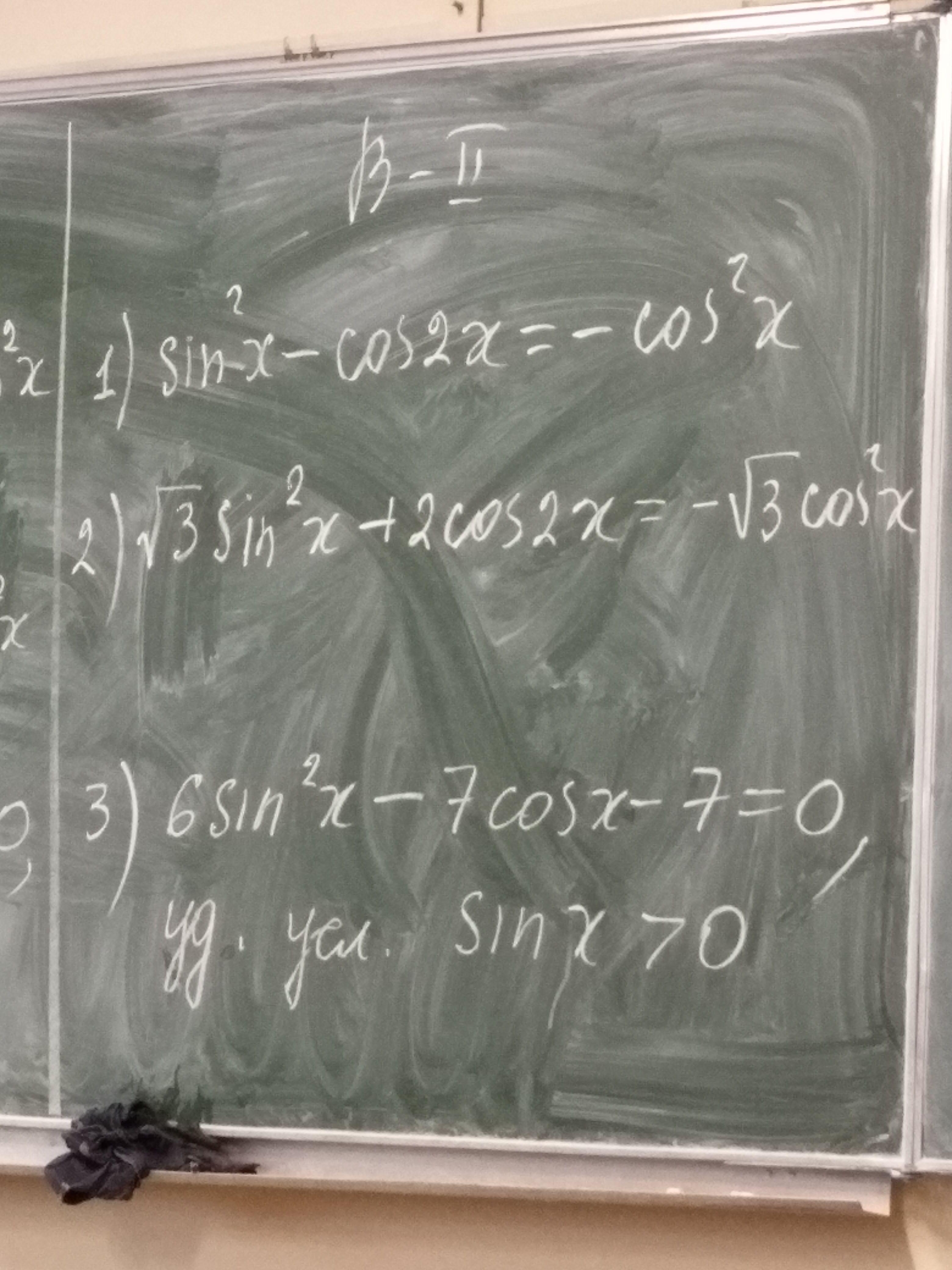
Ответы 6
-
Если нужно найти решения уравнения на каком- то промежутке, то их можно искать на окружности. А у Вас задания, в которых нужно просто решить уравнения.
-
Автор:
nonausul - 6 лет назад
-
0
-
-
Спасибо огромное! Теперь всё ясно
-
Автор:
loreleioneal - 6 лет назад
-
0
-
-
Пожалуйста
-
Автор:
champzegl - 6 лет назад
-
0
-
-
https://znanija.com/task/32425970
-
Автор:
danteguerrero - 6 лет назад
-
0
-
-
помогите пожалуйста
-
Автор:
londynroman - 6 лет назад
-
0
-
-
1) Sin²x - Cos2x = - Cos²x
(Sin²x + Cos²x) - Cos2x = 0
1 - Cos2x = 0
Cos2x = 1
2x = 2πn, n ∈ z
x = πn , n ∈ z
2) √3Sin²x + 2Cos2x = - √3Cos²x
(√3Sin²x + √3Cos²x) + 2Cos2x = 0
√3(Sin²x + Cos²x) + 2Cos2x = 0
√3 + 2Cos2x = 0
2Cos2x = - √3
3)6Sin²x - 7Cosx - 7 = 0
6(1 - Cos²x) - 7Cosx - 7 = 0
6 - 6Cos²x - 7Cosx - 7 = 0
- 6Cos²x - 7Cosx - 1 = 0
6Cos²x + 7Cosx + 1 =0
- 1 ≤ Cosx ≤ 1
1) Cosx = - 1
x = π + 2πn , n ∈ z
Не подходит, так как Sinx > 0
-
Автор:
samsondaugherty - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Срочно очень нужно, есть еще вторая часть этого теста, тоже у меня в вопросах.
-
Напишите структурные формулы и назовите по другой номенклатуре
4-изопропил-3,4-диметилгептан
-
Предмет:
Химия -
Автор:
londoncalderon - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Укр.мова впр.430 заболотний
-
Предмет:
Українська мова -
Автор:
yosef9kds - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Можете скинуть соч по английскому за 3 класс, 4 четверть. Буду очень благодарна
-
Предмет:
Английский язык -
Автор:
jacobs - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
