-
Установить, сходится или расходится знакочередующийся ряд, если сходится, то выяснить каким образом: абсолютно или условно. Помогите пожалуйста с решением! Номер 8.
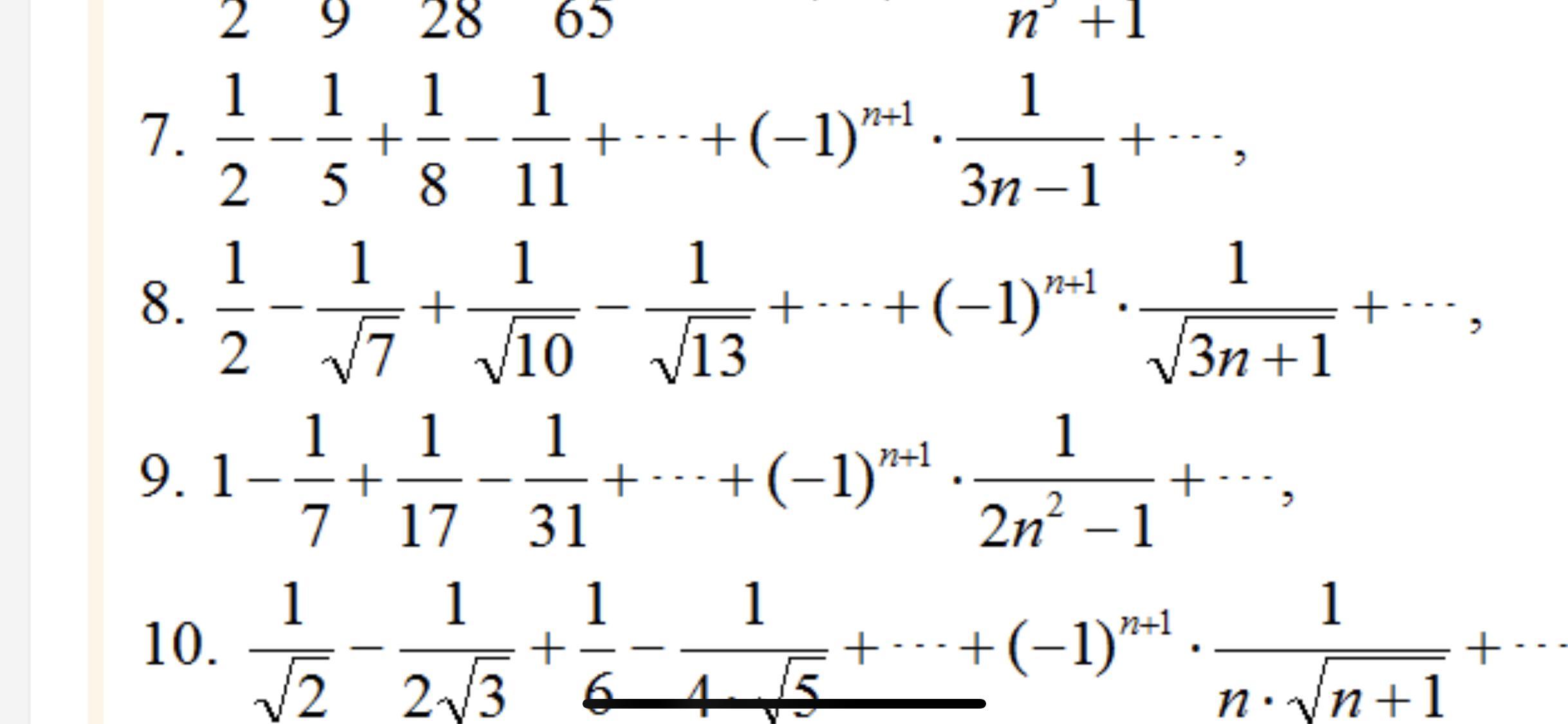
-
Предмет:
Алгебра -
Автор:
finleymw1o - 6 лет назад
-
Ответы 1
-
Ответ:
условно сходится
Объяснение:
Для выяснения сходимости ряда используем признак Лейбница.
Очевидно, что
1.
, так как с увеличением номера n увеличивается знаменатель, а с ростом знаменателя дробь становится все меньше и меньше;
2.
Надеюсь, данный факт ясен.
Два условия выполнены, следовательно, ряд по признаку Лейбница сходится.
Выясним вопрос относительно абсолютной сходимости. Для этого нужно рассмотреть соответствующий ряд из модулей исходного ряда.
Напомню, что модуль "съедает" множитель вида
. Значит, общий член нового ряда имеет вид
.
Для установления сходимости данного ряда используем интегральный признак Коши. Это можно сделать, поскольку действительнозначная функция
неотрицательна, непрерывна и убывает на интервале
Можно рассмотреть несобственный интеграл. Исследуем его на сходимость. подробности в приложенном файле.
Итак, получена бесконечность, стало быть, несобственный интеграл расходится.
Ряд сходится либо расходится вместе с несобственным интегралом. То есть, расходится.
Таким образом, сам ряд сходится. Но ряд из модулей расходится, что исключает абсолютную сходимость ряда. А сходящийся ряд, не сходящийся абсолютно, сходится условно.

-
Автор:
bambino3mle - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Ширина прямоугольного паралелипипида 3,8 метра что на 1,2 метра меньше длинны. Найти обьем паралелипипида
-
Предмет:
Математика -
Автор:
buzzdvhk - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Укажіть неправильне твердження
А) точка перетину діагоналей паралелограма є його центром симетрій
Б) будь який трикутник має 3 осі симетрії
В) Ромб має дві осі симетрії
Г) Рівні фігури переводяться одна в одну переміщенням
-
Предмет:
Геометрия -
Автор:
dravenwilkerson - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
[tex](x + y - 2c)(x + y + 2c) \\ (a + 1) {}^{3}(a - 1) {}^{3} \\ (a + 1) {}^{2}(a - 1) {}^{2} \\(a + 1)(a + 2)(a - 1)(a + 2) \\ [/tex]
умножь многочлены, пользуясь формулами сокращенного умножения -
твір розум "Якою має бути людина ідеальною чи індивідуальною"
-
Предмет:
Українська література -
Автор:
gilliant8vr - 6 лет назад
-
Ответов:
0 -
Смотреть
-
