-
Логарифмическое неравенство по переменному основанию.
Решите, пожалуйста, расписывая, подробно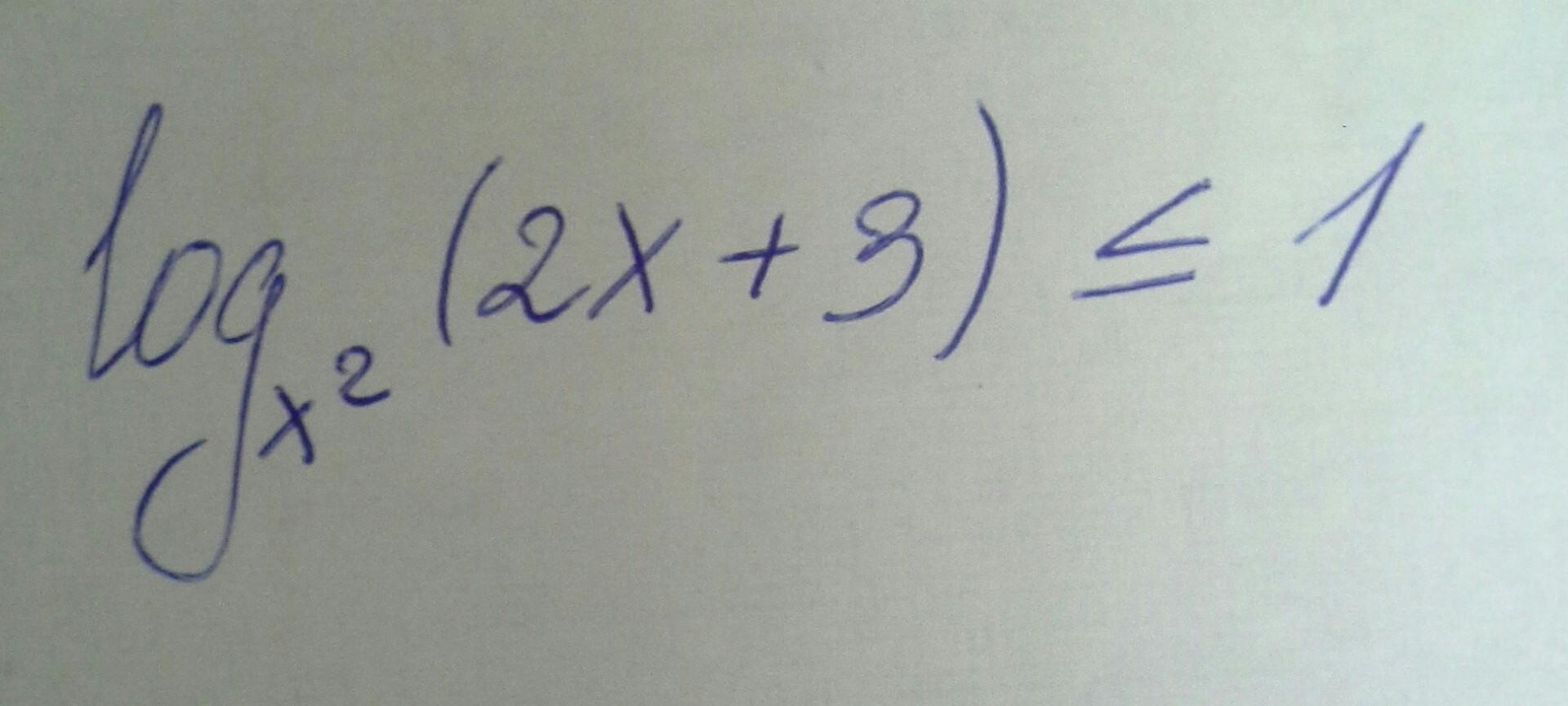
-
Предмет:
Алгебра -
Автор:
madeleine4pv4 - 6 лет назад
-
Ответы 2
-
log (x²) (2x + 3) ≤ 1
ОДЗ x²>0 x≠0
x²≠1 x≠-1 x≠1
2x+3 > 0 x>-3/2
log f(x) g(x) ≤ log f(x) h(x) аналогичен (f(x) - 1)(g(x) - g(x)) ≤ 0
log (x²) (2x + 3) ≤ log (x²) x²
(x² - 1)(2x + 3 - x²) ≤ 0
(x - 1)(x+1)(x² - 2x -3)≥0
разложим x² - 2x -3 =(x+1)(x-3) D=4 + 12 = 16 x12=(2+-4)/2 = -1 3
(x - 1)(x+1)(x + 1)(x -3) ≥ 0
(x + 1)²(x - 1)(x -3) ≥ 0
применяем метод интервалов
++++++++[-1] +++++++ [1] ------------ [3] ++++++++++++
x∈(-∞ 1] U [3 +∞)
+ ОДЗ x>-3/2 x≠ 0 x≠-1 x≠1
Ответ x∈(-3/2 -1) U (-1 0) U (0 1) U [3 +∞)
-
Автор:
oliveouwo - 6 лет назад
-
0
-
-
Ответ: x∈(-1,5;-1)U[3;+∞).
Объяснение:
logₓ²(2x+3)≤1
ОДЗ: x²>0 ⇒ x≠0 x²≠1 x≠-1 x≠1 2x+3>0 2x>-3 x>-1,5 ⇒
x∈(-1,5;-1 )U(-1;0)U(0;1)U(1;+∞).
logₓ²(2x+3)≤logₓ²(x²)
1. x∈(-1,5;-1)U(1;+∞)
2x+3≤x²
x²-2x-3≥0
x²-2x-3=0 D=16 √D=4
x₁=3 x₂=-1 ⇒
(x+1)(x-3)≥0
-∞__+__-1__-__3__+__+∞ x∈(-∞;-1)U[3;+∞) ⇒
x∈(-1,5;-1)U[3;+∞).
2. x∈(-1;0)U(0;1)
2x+3≥x²
x²-2x-3≤0
x²-2x-3=0 D=16 √D=4
x₁=3 x₂=-1 ⇒
(x+1)(x-3)≤0
-∞__+__-1__-__3__+__+∞ x∈(-1;3]. ⇒
x∈(-1;0)U(0;1).
Согласно ОДЗ: x∈(-1,5;-1)U(-1;0)U(0;1)U[ 3;+∞).
-
Автор:
friday - 6 лет назад
-
0
-
-
Добавить свой ответ
-
(37500+2064)+я=100000
-
Предмет:
Математика -
Автор:
maxwell743 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
14. Какая река относится к бассейну Северного Ледовитого океана?
1)Амур; 2)Ангара; 3) Волга; 4) Анадырь
15. Где в России самые плодородные почвы?
1) в Предкавказье; 2) в Предуралье; 3) на Камчатке; 4) на Валдайской Возвышенности
Решить хоть что-нибудь, пожалуйста -
(3,17+0,77:1,4)×3,5-4,216
Срочно, пожааааалуйста-
Предмет:
Математика -
Автор:
cassidygreene - 6 лет назад
-
Ответов:
8 -
Смотреть
-
-
В первый час автобус проехал 4/9 всего пути, во второй час проехал 4/10 ОТ ОСТАЛЬНОГО пути, в 3 час ? оставшийся путь. Сколько всего проехал автобус, если весь путь 112 1/2?
-
Предмет:
Математика -
Автор:
guidozft8 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
