Задать вопрос Регистрация
Помочь другим

  • Вычислить предел функции, используя умножение на сопряженное выражение

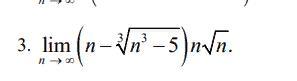
    question img

Ответы 1

  • Ответ:

    Объяснение:

    \lim\limits_{n \to \infty}\left(n-\sqrt[3]{n^3-5} ight)n\sqrt{n}=\lim\limits_{n \to \infty}\frac{\left(n-\sqrt[3]{n^3-5} ight)(n^2+n\sqrt[3]{n^3-5}+\sqrt[3]{(n^3-5)^2})\cdot n\sqrt{n}}{n^2+n\sqrt[3]{n^3-5}+\sqrt[3]{(n^3-5)^2}} =\\=\lim\limits_{n \to \infty}\frac{\left[n^3-\left(n^3-5ight)ight]\cdot n\sqrt{n}}{n^2+n\sqrt[3]{n^3-5}+\sqrt[3]{(n^3-5)^2}}=\lim\limits_{n \to \infty}=5\lim\limits_{n \to \infty}\frac{n^{\frac{3}{2}}}{n^2+n\sqrt[3]{n^3-5}+\sqrt[3]{(n^3-5)^2}} = 0

    Старшая степень числителя равна 3/2, а старшая степень знаменателя равна 2. Следовательно, при стремлении n к бесконечности, знаменатель растёт быстрее числителя и предел равен 0.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years