-
Отдаю все баллы, которые есть. Очень нужно решение. Если сможете, напишите на листке, мне просто понять, как это делать.
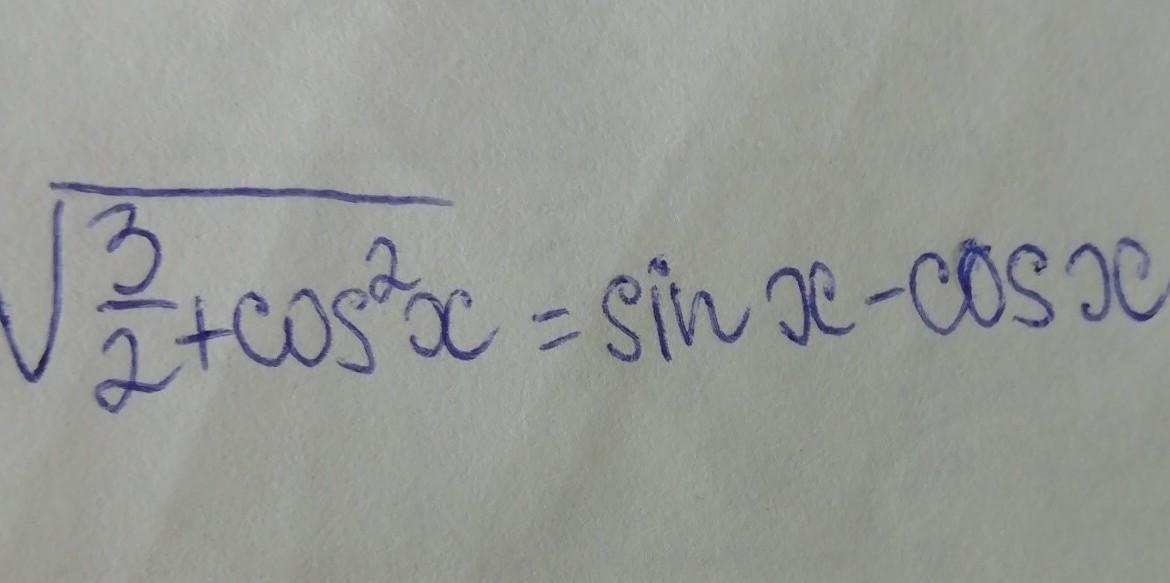
-
Предмет:
Алгебра -
Автор:
basileo6ozg - 6 лет назад
-
Ответы 6
-
Ограничение на правую часть дает множество , на котором возведение в квадрат правомерно , но это не ОДЗ , уберите пожалуйста эту аббревиатуру , решения вы пишете с периодом pin , но , например 7pi/4 решением быть не может , так как тогда правая часть уравнения отрицательна
-
Автор:
baby bird7h7w - 6 лет назад
-
0
-
-
еще одна мелочь - arcctg (-3)
-
Автор:
freckles - 6 лет назад
-
0
-
-
Не доступен режим редактирования
-
Автор:
gavin - 6 лет назад
-
0
-
-
только уравнение имеет решение , если... ( смысл оно имеет при всех х ) и для arcctg ( - 3 ) также период будет 2pin
-
Автор:
chicagnhs - 6 лет назад
-
0
-
-
Отправляйте на исправление
-
Автор:
bishop23 - 6 лет назад
-
0
-
-
Уравнение имеет решение, если sinx - cosx ≥ 0; √2sin(x - π/4) ≥ 0; sin(x - π/4) ≥ 0; 2πn ≤ x - π/4 ≤ π + 2πn, n∈Z; π/4 + 2πn ≤ x ≤ 5π/4 + 2πn, n∈Z.
1,5 + cos²x = (sinx - cosx)²;
1,5 + cos²x = sin²x + cos²x - 2sinxcosx;
1,5 + cos²x = 1 - 2sinxcosx;
cos²x + 2sinxcosx +0,5 = 0;
2cos²x + 4sinxcosx + 1 = 0| : sin²x;
2ctg²x + 4ctgx + 1/sin²x = 0;
2ctg²x + 4ctgx + 1 + ctg²x = 0;
3ctg²x + 4ctgx + 1 = 0;
Замена: ctgx = t/3
t² + 4t + 3 = 0;
t₁ = -1; t₂ = -3
Обратная замена:
ctgx = -1 или ctgx = -1/3
x₁ = 3π/4 + πn, n∈Z; x₂ = arcсtg(-1/3) + πn, n∈Z.
Данное уравнение удовлетворяют значения х₁ = 3π/4 + 2πn, n∈Z; x₂ = arcсtg(-1/3) + 2πn = -arcсtg(1/3) + π(2n+1), n∈Z.
Ответ: 3π/4 + 2πn, n∈Z; -arcctg(1/3) + π(2n + 1), n∈Z.
-
Автор:
fancy - 6 лет назад
-
0
-
-
Добавить свой ответ
-
СН2ОН-СНОН -СНОН -СНОН -СНОН -СН=О + Ag(NH3)2OH =2 NH3 +H2O +Ag +
CH2OH-СНОН -СНОН -СНОН -СНОН -COOH
КАК НАЗЫВАЕТСЯ РЕАКЦИЯ? ДАМ 15 БАЛЛОВ -
Как называли угощение которое ел пьер после бородинского сражения
В романе Толстого война и мир-
Предмет:
Литература -
Автор:
tessahudson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Масса Насти составяет 35% массы мамы. Наидите массу мамы, если масса Насти 28кг
Решите пожалуйста
-
Предмет:
Математика -
Автор:
titan10 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Внешний угол при основании равнобедренного треугольника равен 115°. Найдите углы треугольника.
