-
Найти площадь фигуры ограниченной отрезками.
Функция: y = -2x^2 + 4x + 3
ограниченная прямыми:
y = 5
x = 0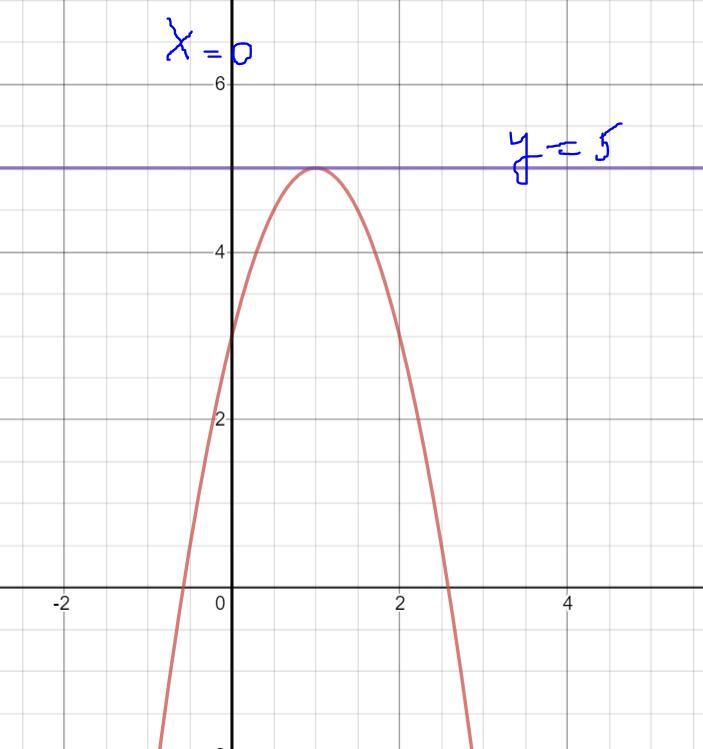
Ответы 3
-
А мы разве ищем площадь не того маленького треугольничка от 0 до 1 который как раз ограничен всеми линиями? Как вообще определять какую фигуру мы ищем
-
Автор:
philiponw4 - 6 лет назад
-
0
-
-
Это должно быть оговорено в задании, При правильном задании ясно, где расположена искомая площадь.
-
Автор:
donald362 - 6 лет назад
-
0
-
-
Будем считать, что ограничением есть только х = 0, так как прямая у = 5 находится за пределами площади, ограниченной параболой
y = -2x^2 + 4x + 3.
Для ограничения площади при пересечении параболой с осью Ох надо найти координаты точки пересечения параболы с осью Ох, при этом у = 0. Приравняем -2x^2 + 4x + 3 = 0. Д - 16 - 4*(-2)*3 = 40.
х = (-4 + √40)/(2*(-2)) = 1 +√(40/16) = 1 + √2,5 (правая точка).
Левую точку не определяем, так как задано х = 0.
Площадь определяем по интегралу:
-
Автор:
dariabidv - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите, нужно 3 задание
В нём нужно поставить правильно слова-
Предмет:
Английский язык -
Автор:
chanelwtyt - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решить уравнение (X+92)×9=2718
-
Предмет:
Математика -
Автор:
kevin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Переведите следующие предложения (очень срочно)
1 The engineering plastics are now challenging the domain traditionally held by metals: truly load-bearing, structural parts.
2 The products produced by our chemical plant are of very high quality.
3 There are two kinds of materials used in engineering – metals and non-metals.
4 When added to steel certain elements can improve its properties.
5The experiment being demonstrated, all the students watched it with great
attention.
6 Weather permitting, we shall go for a walk.
7 The students having many labs with modern equipment at our institute, scientific
research can be conducted at a very high level.
8 This scientist being in our country got interested in our system of education-
Предмет:
Английский язык -
Автор:
lassiemathis - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решить уравнение (X-92)×9=2718
-
Предмет:
Математика -
Автор:
siennadowns - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
