-
Найдите промежутки, на которых функция = х^2 / x+1 убывает.
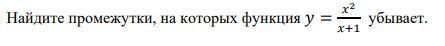
Ответы 1
-
Функция y убывает там, где y' < 0
-
Автор:
jennahamilton - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
для приготовления кофейного на 7 частей кофе берут 6 частей цикория, 4 части желудей и 1 часть каштанов. Сколько напитка ( в кг ) изготовлено , если кофе и цикория вместе израсходовали 26 кг? СРОЧНО помогите с этим заданием!
-
Предмет:
Химия -
Автор:
estherbrewer - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
III.раскройте скобки употребите глагол в соответствующем времени.
IV. поставьте вопрос к предложения употребив указанное вопросительное слово
-
Предмет:
Английский язык -
Автор:
double double - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
печенье сладкое, а конфеты ещё ...
-
Предмет:
Русский язык -
Автор:
dylanrwlj - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
Розкрити зміст вислову "Рукописи не говорять",назвати автора та твір,де використано цю думку.
-
Предмет:
Литература -
Автор:
rockettevxov - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
