-
SOS SOS Знайти площу фігури обмежиної лініями у=lin x, y=lin3x,
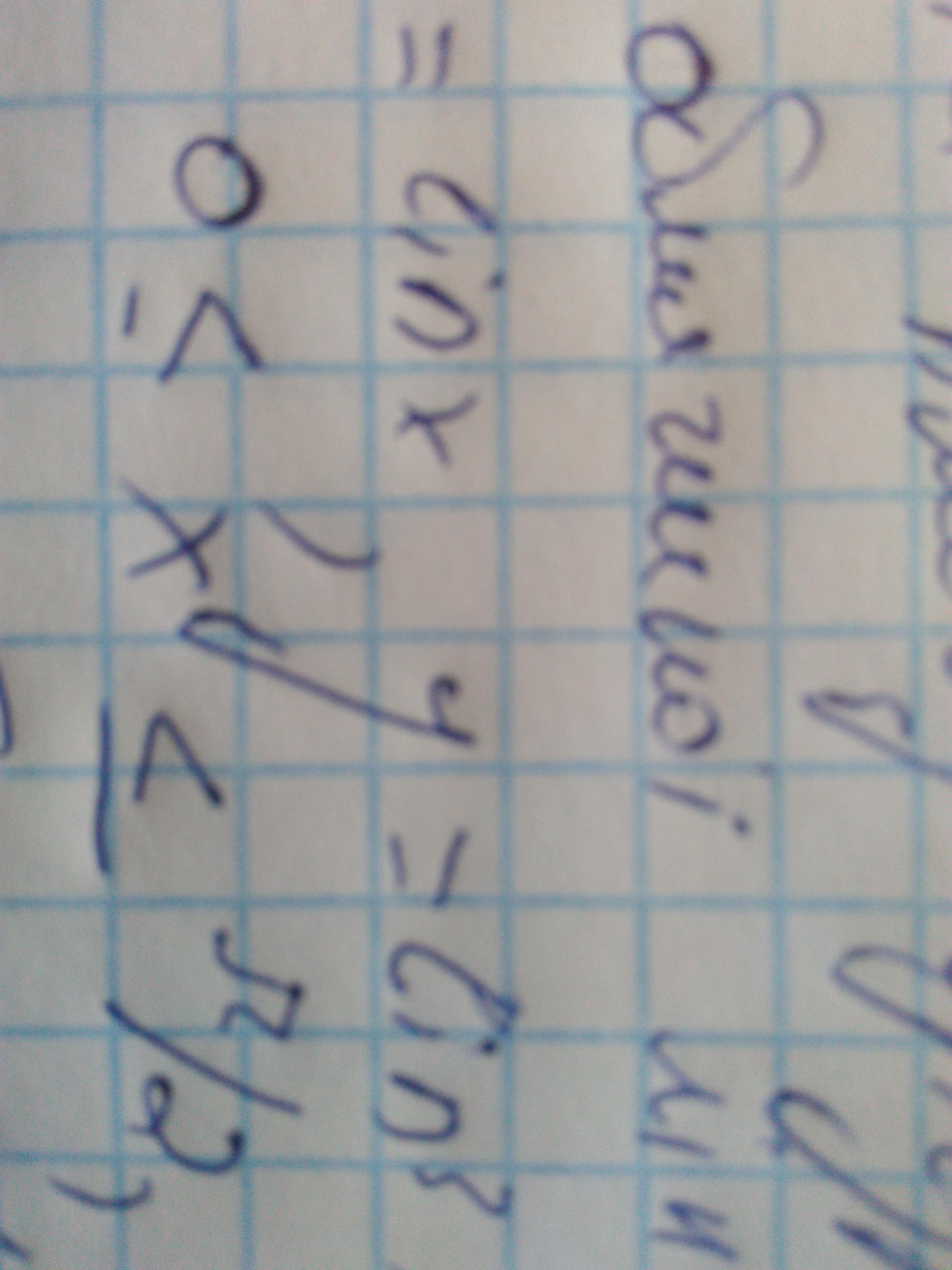
-
Предмет:
Алгебра -
Автор:
dropouttiw0 - 6 лет назад
-
Ответы 6
-
Дякую
-
Автор:
alfredoclark - 6 лет назад
-
0
-
-
Ти вирішив усі 3?
-
Автор:
punk77 - 6 лет назад
-
0
-
-
Решение неверно! Попутаны функции sin(x) и sin(3x). Вершина последней х = pi/6. Точка пересечения pi/4, в точке pi/2 вершины друг против друга. Площадь поэтому состоит из двух участков.
-
Автор:
madeline - 6 лет назад
-
0
-
-
А Ви можете рішити і кинути фото?
-
Автор:
natividadholt - 6 лет назад
-
0
-
-
Ответ:
Объяснение:
===============

-
Автор:
figarocortez - 6 лет назад
-
0
-
-
Дано: найти площадь между линиями у=sin(x), y=sin(3x) в пределах от х =0 до х = π/2.
Находим точку пересечения линий - это условие sin(x) = sin(3x).
Синус тройного угла равен: sin(3x) = 3sin(x) - 4sin³(x). Подставим:
sin(x) = 3sin(x) - 4sin³(x).
4sin³(x) = 2sin(x).
4sin³(x) - 2sin(x) = 0. Сократим на 2.
2sin³(x) - sin(x) = 0. Вынесем за скобки.
sin(x)(2sin²(x) - 1) = 0. Приравниваем нулю каждый множитель.
sin(x) = 0. х = πк, к ∈ Z.
2sin²(x) - 1, sin(x) = +-1/√2.
x = 2πк +- (π/4), x = 2πк +- (3π/4).
Из этих корней выбираем тот, что находится между 0 и π/2.
Это х = 1/√2 или х = √2/2.
Заданная площадь этой точкой делится на 2 участка.
.
В числовом выражении S1 ≈ 0,27614.
Аналогично находим:
В числовом выражении S2 ≈ 0,94281.
Ответ: площадь равна (1/3)*(4√2 - 2) ≈ 1,21895.

-
Автор:
lila - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Подскажите короткое очень короткий пересказ Дон Кихот для читательского дневника
-
Предмет:
Литература -
Автор:
marley41 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помощь оч нужна, но только все по действиям нужно!!!!!!!!! 15 баллов
-
Предмет:
Математика -
Автор:
brooklynnjhzg - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Найдите запирающие напряжение, если максимальная кинетическая энергия фотоэлектронов равна 5,0 эВ
-
помогите пожалуйста выбрать правильную букву a ) b) or c)
-
Предмет:
Английский язык -
Автор:
hanktp89 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
