Постройте график функции
y=4|x-3|-xˆ2+8x-15
определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки

Ответ:

Объяснение:

1) при х≥3

y=4|x-3|-xˆ2+8x-15=4(x-3)-xˆ2+8x-15=4x-12-xˆ2+8x-15=-х^2+12x-27

координаты вершины 12/2=6; y(6)=-36+72-27 (6;9)

пересечение с осью ОХ -х^2+12x-27=0 х^2-12x+27=0

х₁-₂=(12±√144-108)/2=(12±6)/2={3;9}

2)  при х<3

y=4|x-3|-xˆ2+8x-15=-4(x-3)-xˆ2+8x-15=-4x+12-xˆ2+8x-15=-х^2+4x-3

координаты вершины 4/2=2; y(2)=-4+8-3=1  (2;1)

пересечение с осью ОХ х^2+4x-3=0 х^2-4x+3=0

х₁-₂=(4±√16-12)/2=(4±2)/2={1;3}

в точке 3 два графика пересекаются

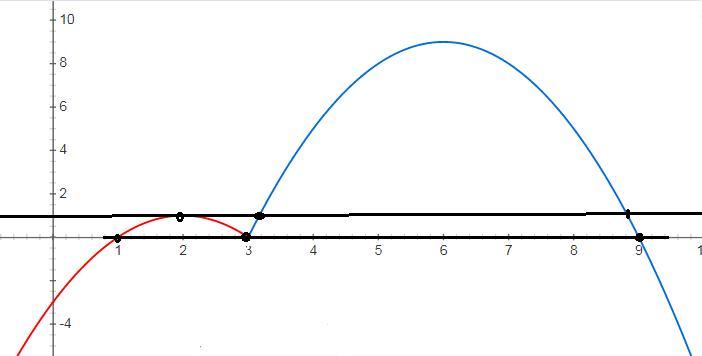
3) построение

при x<3 строим график у=-х^2+4x-3

при х≥3 строим график у=-х^2+12x-27

по вершинам и точкам пересечения с осью ОХ

4) y=m имеет с графиком ровно три общие точки при

m=0

m= 2 (вершина графика у=-х^2+4x-3)