-
Помогите пожалуйста с решением интегралов, очень срочно!!!
За задание 98 баллов!!!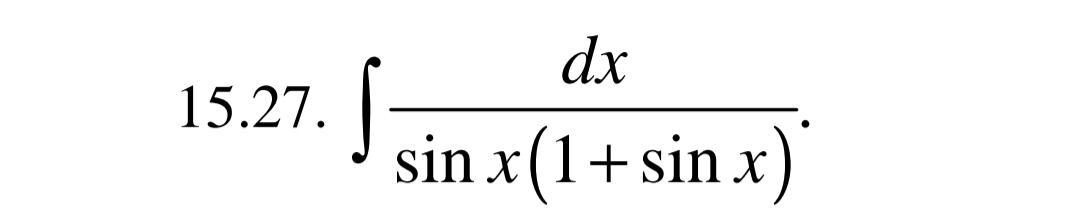
-
Предмет:
Алгебра -
Автор:
dexter9odh - 6 лет назад
-
Ответы 1
-
Преобразуем знаменатель подынтегральной функции:
sin(x)*(1+sin(x) ) = 2*sin(x/2)*cos(x/2)* (sin(x/2)+cos(x/2) )^2=
=2*cos^4(x/2)*tg(x/2) *(1+tg(x/2))^2
dx/(sin(x) *(1+sin(x) ))= dx/(cos^2(x/2) )/2*cos^2(x/2)*tg(x/2)*(1+tg(x/2))^2
cos^2(x/2)+sin^2(x/2)=1
1+tg^2(x/2)=1/cos^2(x/2)
int( (1+tg^2(x/2))*d(tg(x/2))/ ( tg(x/2)*(1+tg(x/2))^2) )
tg(x/2)=t
int( (1+t^2)*dt/t*(1+t)^2)
(1+t^2)/(t*(t+1)^2) = ( (t+1)^2-2t)/(t*(t+1)^2) =1/t -2/(1+t)^2
int( (1+t^2)*dt/t*(1+t)^2)=int( (1/t -2/(1+t)^2)dt)= ln(t)+2/(1+t)+c= ln(tg(x/2))+2/(1+tg(x/2) )+c
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Установіть послідовність подій у творі:
1. Ромео вбиває Тібальта.
2. Смерть Ромео і Паріса.
3. Ромео домовляється з братом Лоренцо про таємне вінчання.
4. Вигнання Ромео з Верони.
5. Удавана смерть Джульєтти.
6. Зіткнення на площі слуг Монтеккі і Капулетті.
-
Предмет:
Литература -
Автор:
kaiden0ddl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
4 1/8 + 5/12 решите пожалуйста срочно мне нужно
-
Предмет:
Математика -
Автор:
laurelcowan - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Какой груз может быть подвешен на тросе 5 см при запасе прочности 10, если предел прочности троса 400 МПа
-
Перечень жизненно необходимых качеств человека способствующих поднятию общего уровня культуры в области безопасности а так же когда и где они должна начинать формироваться
-
Предмет:
ОБЖ -
Автор:
heliodoroi0bl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
