-
Помогите пожалуйста.
[tex]log _{0.2} ( \frac{2}{x-2} )\leq log _{0.2} (5-x)[/tex]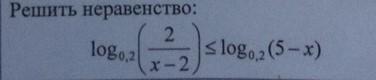
-
Предмет:
Алгебра -
Автор:
sofiascott - 6 лет назад
-
Ответы 2
-
Решение во вложении.
Ответ: (5; +бесконечность)

-
Автор:
dariocisneros - 6 лет назад
-
0
-
-
㏒₀,₂(2/(х-2))≤㏒₀,₂(5-х); ОДЗ неравенства х строго больше 2, но меньше пяти. т.к. основание больше 0, но меньше 1, то меняем знак неравенства по отношению к агрументу. Получим (2/(х-2))≥(5-х); (2-(5-х)(х-2))/(х-2)≥0
(2-(5х-10-х²+2х)/(х-2)≥0; (2-5х+10+х²-2х)/(х-2)≥0; (х²-7х+12)/(х-2)≥0 ; х²-7х+12=0, по Виета х=3, х=4. неравенство при данном ОДЗ равносильно такому (х-4)(х-3)(х-2)≥0; х≠2
это неравенство решим методом интервалов.
___2_______3_________4______________
- + - +
Решением с учетом ОДЗ будет (2;3]∪[4;5)

-
Автор:
zion46 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
4. Какое количество теплоты выделится при полном сгорании 2 кг каменного угля, если
его удельная теплота сгорания составляет 3* 10 Дж/кг?
А. 1.5*10^7 Дж Б. 6*10^7 Д. В. 5 *10^7 Дж Г. 2/3* 10^-7 Дж.
5. Отрицательно заряженную палочку поднесли телу. При этом тело отталкнулось от
палочки. Как оно было заряжено?
А. Положительно Б. Отрицательно В. Было не заряжено Г. В любом случае тело
должно было отталкнуться.
7. Чему равна сила тока в проводнике сопротивлением 20 Ом, находящемся под
напряжением 100В?
А. 5А Б. 2 000A В. 0.2А Г. 120A
8. Магнитную стрелку поднесли к южному полюсу магнита. Как будет вести себя эта
стрелка?
A. Не будет реагировать Б. Повернется северным полюсом В. Повернется
южным полюсом -
Решите а,б,в,г.Пожалуйста
известно, что п/2<а<п. Найдите:
а)sina ,если cosa =-0,6 -
1. Определенный артикль (случаи употребления). 2. Past Simple Tense: случаи употребления, слова-индикаторы, грамматическое образование(утверждение, общий вопрос, краткие ответы).
-
Предмет:
Английский язык -
Автор:
astronelson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Как известно световые лучи обратимы. Как это утверждение можно применить при использовании формулы тонкой линзы?
How much to ban the user?
1 hour
1 day
100 years
