-
Доказать, что при всех допустимых значениях а справедливо равенство:
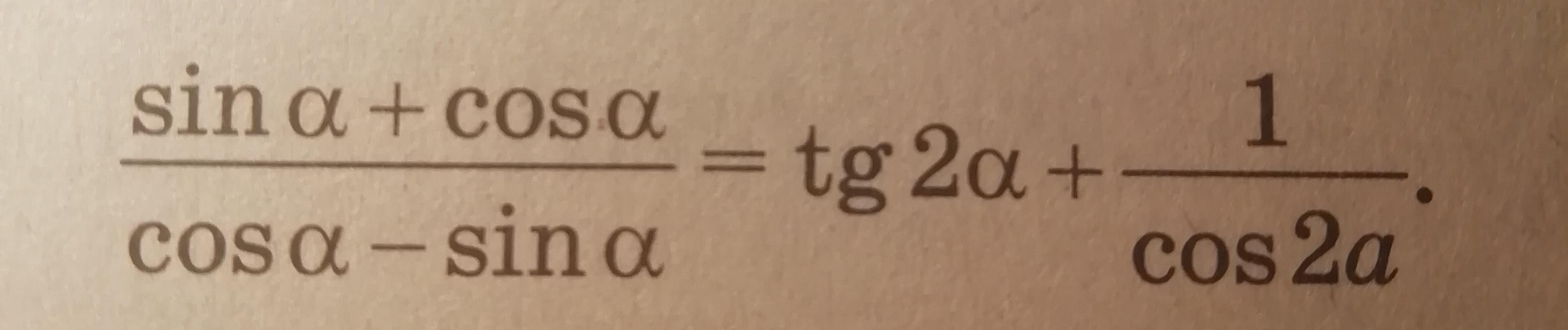
Ответы 2
-
cos (2a) = cos² (a) - sin² (a)
tg (a) = sin (a) / cos(a)
sin (2a) = 2sin(a)cos(a)
sin² a + cos² a = 1
======================
tg (2a) + 1/cos(2a) = sin(2a) / cos(2a) + (sin²(a) + cos²(a))/cos(2a) =
= (sin²(a) + 2sin(a)cos(a) + cos²(a)) / (cos²(a) - sin²(a)) = (sin(a) + cos(a))²/(cos(a)-sin(a))(cos(a)+sin(a)) = (sin(a) + cos(a))/(cos(a) - sin(a)) доказали
-
Автор:
orlandowqjm - 6 лет назад
-
0
-
-
Из левой части получим правую для чего домножим числитель и знаменатель левой части на сумму (sinα+cosα)
((sinα+cosα)²)/((cosα-sinα)(sinα+cosα)) Числитель разложим по формуле
(а+в)²=а²+2ав+в², а знаменатель по формуле (а-в)*(а+в)=а²- в², и почленно разделим числитель на знаменатель, предварительно применив формулу косинуса двойного аргумента cos²α-sin²α=cos2α; синуса двойного аргумента 2sinα*cosα= sin2α и основное тригонометрическое тождество sinα²+cos²α=1.
(sinα²+2sinα*cosα+cos²α)/(cos²α-sin²α)=(1+sin2α)/(cos2α)=
1/cos2α+(sin2α)/(cos2α)=tg2α+(1/cos2α) , что и требовалось доказать.
-
Автор:
tobiasgncf - 6 лет назад
-
0
-
-
Добавить свой ответ
-
РЕБЯТА ПОМОГИТЕ!!!(КТО ЛИБИТ ФУТБОЛ)
Вопрос: Чего вы хотели добираться
в футболе???
-
Предмет:
Физкультура и спорт -
Автор:
alishabrennan - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Объем водорода (при н.у.), который необходим для синтеза 200 л аммиака
равен
А 300 л
Б 100 л
В 200 л
Г 150 л-
Предмет:
Химия -
Автор:
hamzaknapp - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Расположите в правильном порядке пункты инструкции по приготовлению микропрепарата животной клетки. В ответе запишите соответствующую последовательность цифр.
1)
протрите салфеткой предметное и покровное стёкла
2)
капните раствор йода на приготовленный препарат и накройте покровным стеклом
3)
поместите снятую слизь на предметное стекло
4)
зарисуйте животные клетки, обозначив мембрану, цитоплазму и ядро
5)
рассмотрите микропрепарат под микроскопом
6)
возьмите чистый шпатель и с лёгким нажатием проведите им по твёрдому нёбу или дёснам-
Предмет:
Биология -
Автор:
lucianofr20 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
КЛЕТКИ
Первыми на пути исторического развития появились организмы, имеющие мелкие клетки с очень простой внутренней структурой, – __________ (А) клетки. Лишь позднее возникли более крупные и сложно устроенные клетки – __________ (Б). Первые не имели ядра. Такие клетки –
у __________ (В) и синезелёных. Из более сложных клеток построены растения, животные и __________ (Г).
ПЕРЕЧЕНЬ ТЕРМИНОВ:
1)
гриб
2)
прокариот
3)
цитоплазма
4)
вирус
5)
коацерват
6)
одноклеточное животное
7)
бактерия
8)
эукариот
