Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста, с решением уравнения. У меня упорно не хотят сходится ответы

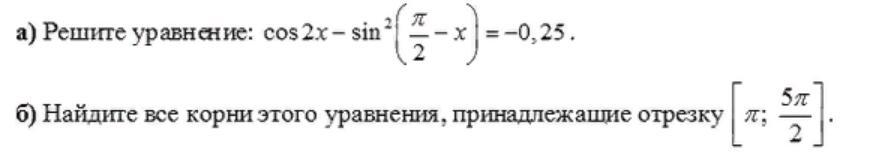
    question img

Ответы 7

  • а, ок

    • Автор:

      hazel7rf3
    • 5 лет назад
    • 0
  • :)
  • А если косинус двойного угла раскрыть как cos^2x-sin^2x, то косинусы сократятся
  • ну да, и получатся те же самые точки, только через синус

    • Автор:

      hernandez
    • 5 лет назад
    • 0
  • Но все равно спасибо!

    • Автор:

      layne
    • 5 лет назад
    • 0

  • /////////////////////////

    answer img

  • cos2x-sin^2(\frac{\pi}{2}-x)=-0,25\\\\cos2x-cos^2x=-0,25\\\\\underbrace {cos^2x-sin^2x}_{cos2x}-cos^2x=-0,25\; \; \; \Rightarrow \; \; \; sin^2x=0,25\\\\\star \; \; sin^2x=\frac{1-cos2x}{2}\; \; \star \\\\\frac{1-cos2x}{2}=\frac{1}{4}\; \; \to \; \; \; 1-cos2x=\frac{1}{2}\; \; ,\; \; cos2x=\frac{1}{2}\\\\2x=\pm arccos\frac{1}{2}+2\pi n\; ,\; n\in Z\\\\2x=\pm \frac{\pi }{3}+2\pi n\; ,\; n\in Z\\\\\underline {x=\pm \frac{\pi }{6}+\pi n\; ,\; n\in Z}

    b)\; \; x\in [\pi ;\frac{5\pi}{2}\, ]:\\\=1\; \; ,\; \; x_1=\frac{\pi}{6}+\pi =\frac{7\pi }{6}\in [\pi ;\frac{5\pi}{2}\, ]\; \; ;\; \; x_2=-\frac{\pi}{6}+\pi =\frac{5\pi}{6}otin [\pi ;\frac{5\pi}{2}\, ]\\\=2\; ,\; \; x_3=\frac{\pi}{6}+2\pi =\frac{13\pi }{6}\in [\pi ;\frac{5\pi}{2}\, ]\; ;\; \; x_4=-\frac{\pi}{6}+2\pi =\frac{11\pi }{6}\in [\pi ;\frac{5\pi}{2}\, ]\\\=3\; ,\; x_5=\frac{\pi}{6}+3\pi =\frac{19\pi}{6}otin [\pi ;\frac{5\pi}{2}\, ]\; ;\; \; x_6=-\frac{\pi}{6}+3\pi =\frac{17\p}{6}otin [\pi ;\frac{5\pi}{2}\, ]\\\\\underline {x=\frac{7\pi }{6}\; ,\; \; \frac{11\pi }{6}\; ,\; \; \frac{13\pi }{6}} \\\\Otvet:\; \; a)\; x=\pm \frac{\pi }{6}+\pi n\; ,\; n\in Z\; ;\; \; b)\; x=\frac{7\pi }{6}\; ,\; \; \frac{11\pi }{6}\; ,\; \; \frac{13\pi }{6}\; .

    answer img

    • Автор:

      halle
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years