-
Найти сумму первых пяти членов числовой последовательности
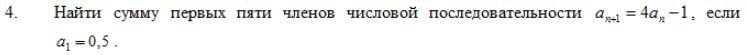
-
Предмет:
Алгебра -
Автор:
nevaehdd2i - 6 лет назад
-
Ответы 2
-
0,5+1+3+11+43=58,5
........
-
Автор:
susie qxg0g - 6 лет назад
-
0
-
-
Ответ: S(n)= ((3a-1)*(4^n-1) +3n)/9
S(5)= 58.5 (при a=0.5)
Объяснение:
Можно решать в лоб и просто найти и сложить все 5 членов.
Используя рекуррентное соотношение: a(n+1)=4*a(n)-1, найдем все все 5 членов:
a(1)=0.5
a(2)=4*0.5-1=1
a(3)=4*1-1=3
a(4)=4*3-1=11
a(5)=4*11-1=43
S(5)=0.5+1+3+11+43=58.5
Но мы решим эту задачу в общем виде.
Cначало попробуем найти формулу n-го члена этой последовательности.
Используем рекуррентное соотношение :
a(n+1)=4*a(n)-1
Запишем первые 3 члена:
a(1)=a1
a(2)=4a1-1
a(3)=4*(4a1-1)-1=16*a1-4a-1=4^2*a1-4a1-1
Можно уже догадаться что формула n члена имеет вид:
a(n)=a1*4^(n-1)-4^(n-2)-4^(n-3)....-4^4 - 4^3 - 4^2- 4- 1
Докажем наше предположение методом математической индукции:
Вычислим значение для n=1 :
a(1)=a1*4^(1-1)=a1*4^0=a1 ( верно)
Предположим, что формула верна для n=k :
a(k)=a1*4^(k-1)-4^(k-2)-4^(k-3).... - 4^2 - 4 - 1
Тогда покажем ее верность для n=k+1
То есть необходимо доказать что:
a(k+1)=a1*4^k -4^(k-1)-4^(k-2)....-4^2-4-1
Поскольку : a(k+1)=4*a(k)-1
a(k+1)=4*(a1*4^(k-1)-4^(k-2)-4^(k-3)....-4^2- 4- 1 )-1= =a1*4^k -4^(k-1)-4^(k-2)....-4^3-4^2-4-1 - (верно)
Таким образом наше предположение доказано.
Заметим, что нашу формулу можно записать так:
a(n)=a1*4^(n-1) + (1+4+4^2+4^3....+ 4^(n-1)+4^(n-2) )
В скобках видим сумму геометрической прогрессии в которой:
b1=1
q=4
Тогда выражение в скобках равно:
S'=(q^(n-1)-1)/(q-1) =(4^(n-1) -1)/(4-1)= (4^(n-1)-1)/3
a(n)= a1*4^(n-1) - (4^(n-1)-1)/3= (3*a1*4^(n-1) -4^(n-1)+1)/3=
= (4^(n-1) *(3a1-1) +1)/3 = 4^(n-1)*(3a1-1) +1/3
Теперь можно найти сумму n членов:
S(n)= 1/3 * (3a1-1)*(1+4+4^2...+4^(n-1) ) +n*(1/3)
Cумма в скобках вновь геометрическая прогрессия:
S''= (4^n -1)/3
S(n)= (3a-1)*(4^n -1)/9 +n/3= ((3a-1)*(4^n -1) +3n)/9
Таким образом формула сумму n-членов ряда заданного рекуррентным соотношением:
a(n+1)=4*a(n)-1
Вычисляется по формуле:
S(n)= ((3a-1)*(4^n -1) +3n)/9
Осталось подставить в формулу начальные данные:
a1=0.5
n=5
3a-1=3*0.5-1=0.5
4^n-1=4^5 -1= 1024-1=1023
S(5)= (0.5 *1023 +15)/9= 58.5
Ответ: S(5)= 58.5
P.S как видим ответ совпал .
-
Автор:
bentley79 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
log7 34,2 + 2log7√10
найти значение выражения -
1. Почему право вершить правосудие автор отдал отчиму Людочки?
2. В чем смысл названия рассказа?
3. Какой нравственный урок содержит произведение В.П.Астафьева?
Ответе пожалуйста кратко и подробно-
Предмет:
Литература -
Автор:
summergz6g - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
сложныЕ ВЫЧИСЛЕНИЯ
98 - 20 - 30-4 0+ (27+6 - 23 =
100-20--(2576) +30- 4 =-
Предмет:
Математика -
Автор:
vicente34 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Реши уравнение: 1\4y +4=20-1\12y
-
Предмет:
Математика -
Автор:
ivyyjhu - 6 лет назад
-
Ответов:
6 -
Смотреть
-
