-
Знайдіть похідну даної функції та обчисліть її значення в даній точці х0 :
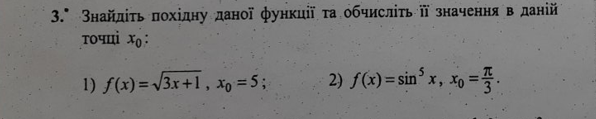
Ответы 1
-
Нам необходимо найти производную следующей функции:
y = sqrt (6 * x + 7)
где sqrt означает корень квадратный.
Для нахождения данной производной нам необходимо:
(xa)' = a * xa-1;
(a)' = 0;
(f(g(x)))' = f(x)' * g(x)'.
Таким образом мы получаем:
y' = (sqrt (6 * x + 7))' = ((6 * x + 7) ^ (1/2))' = ((6 * x + 7) ^ (1/2))' * (6 * x + 7)' = 1/2 * (6 * x + 4) ^ (1/2 - 1) * 6 = 6/2 * (6 * x + 7) ^ (1/2 - 2/2) = 3 * (6 * x + 7) ^ (- 1/2) = 3 / sqrt (6 * x + 7)
Найдем значение данной функции в точке x0 = 3
3 / sqrt (6 * x + 7) = 3 / sqrt (6 * 3 + 7) = 3 / sqrt 25 = 3/5
-
Автор:
Fedoseewa27 - 3 года назад
-
0
-
-
Добавить свой ответ
-
Знайдіть рівняння дотичної до графіка функції f(x)=x^4-2x у точці з абсцисою x0=-1
-
Предмет:
Математика -
Автор:
STIX - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 12, а от большей на 15. Найдите периметр прямоугольника. РЕШЕНИЕ ПОЖАЛУЙСТА!!!!!!!!!!!!
-
найдите точку экстремума функции y=(3x^2-36+63)*e^x-3 СРОЧНО
-
Предмет:
Математика -
Автор:
deniska228232 - 3 года назад
-
Ответов:
1 -
Смотреть
-
-
Грозился что значит?
-
Предмет:
Русский язык -
Автор:
campbello6so - 3 года назад
-
Ответов:
1 -
Смотреть
-
