-
Знайдіть область визначення функції f(x) =5√(log3^2 x-log3x-2)
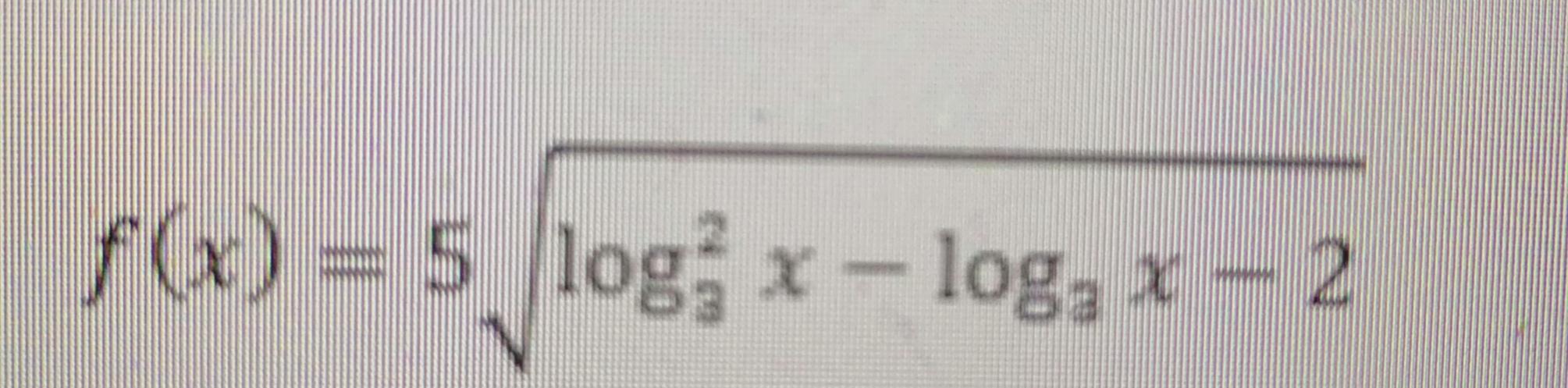
Ответы 1
-
Для того щоб знайти область визначення функції f(x) = 5√(log3^2 x-log3x-2), необхідно знайти множину тих значень x, для яких значення функції є дійсними.
Спочатку замініть log3^2 x на (log3 x)^2:
f(x) = 5√((log3 x)^2 - log3 x - 2)
Далі, розглянемо вираз внутрішнього квадратного кореня: (log3 x)^2 - log3 x - 2. Щоб цей вираз був додатнім, необхідно щоб дискримінант рівняв 0 і більше.
(log3 x)^2 - log3 x - 2 = 0
Розв'яжемо рівняння:
(log3 x)^2 - log3 x - 2 = 0
(log3 x - 2)(log3 x + 1) = 0
Розв'язки рівняння:
log3 x = 2 або log3 x = -1
x = 3^2 = 9 або x = 3^-1 = 1/3
Таким чином, область визначення функції f(x) = 5√(log3^2 x-log3x-2) є множиною х, які знаходяться у діапазоні (1/3, 9]
-
Автор:
guidomiranda - 3 года назад
-
6
-
-
Добавить свой ответ
Еще вопросы
- ДАЮ 100 БАЛОВ Познач та підпиши географічні об’єкти на контурній карті:— острови: Вогняна Земля, Фолклендські (Мальвінські), Малі Антильські, Галапагос;— крайні точки: Гальїнас (пн.), Фрауерд (пд.), Кабу-Бранку (сх.), Паріньяс (зх.)
-
омогите пожалуйста В каком сложноподчинённом предложении есть придаточное изъяснительное? 1. Последнее, что я ещё видел, был Петька, выскочивший на улицу и захлопнувший калитку перед самым носом человека в пальто. 2. Сколько времени прошло, я не помню. 3. У него ничего не клеилось, что бы он ни предпринимал. 4. Поскольку дом был окружён высоким забором, нам пришлось обойти его в поисках калитки. В каком сложноподчинённом предложении есть придаточное изъяснительное? 1. Кругом было так тихо, что по жужжанию комара можно было следить за его полётом. 2. Скажи мне, какие книги ты читаешь, и я скажу, кто ты. 3. Окрик показался Аксинье настолько громким, что она ничком упала на землю. 4. Пыль на улице была такая едкая, что глазам становилось больно
-
Предмет:
Русский язык -
Автор:
babs - 3 года назад
-
Ответов:
1 -
Смотреть
-
- Познач назви рослин, отруєння якими може бути смертельним. Виберіть одну або декілька відповідей: валеріана вороняче око дурман звіробій конвалія алтея
- Алгебра, квадратное уравнение. Надо решить.
How much to ban the user?
1 hour
1 day
100 years
