-
3.Упростить выражение:а) sin2a/ 2tgaб) 1+соs 2a/1-cos2a
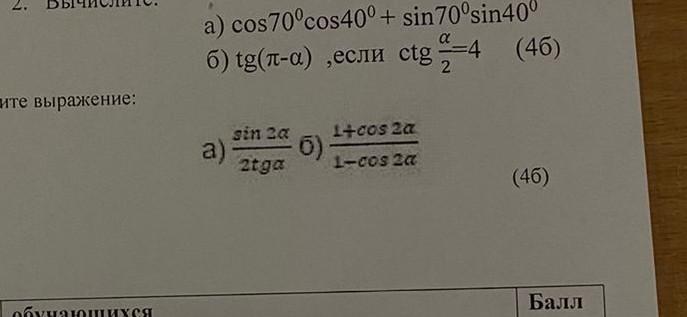
-
Предмет:
Алгебра -
Автор:
immanuelwaller - 2 года назад
-
Ответы 1
-
Ответ:
Объяснение:
А)
Перепишем тангенс через синус и косинус:
tg a = sin a / cos a
Тогда:
sin 2a / 2tg a = sin 2a / (2sin a / cos a) = (sin 2a * cos a) / (2sin a) = cos a / 2
Таким образом, выражение sin 2a / 2tg a упрощается до cos a / 2.
B)
Мы можем воспользоваться формулой сокращения для тригонометрического выражения:
cos 2a = cos² a - sin² a
Тогда:
1 + cos 2a = 1 + cos² a - sin² a
(1 - cos 2a)(1 + cos 2a) = (1 - cos² 2a) = sin² 2a
Таким образом, исходное выражение принимает вид:
(1 + cos 2a) / (1 - cos 2a) = [(1 + cos² a - sin² a) / (2 cos² a)] / [(cos² a - sin² a) / (2 cos² a)] = (1 + cos² a - sin² a) / (cos² a - sin² a) = [(1 + cos² a) - sin² a] / [(1 - sin a)(1 + sin a)] = [(1 + cos a)(1 - cos a)] / [(1 - sin a)(1 + sin a)] = (1 - cos a) / (1 + sin a)
Таким образом, выражение 1 + cos 2a / 1 - cos 2a упрощается до (1 - cos a) / (1 + sin a).
-
Автор:
gissellewiley - 2 года назад
-
7
-
-
Добавить свой ответ
- на опру какой площади надо поставить груз массой 500кг, чтобы произвести давление, равное 25кПа помогите
-
3. Треугольник, с какими сторонами мы смогли построить? а) 7.4,9 b) 9,18,9 c) 6,9,14СРОЧНО
-
Предмет:
Математика -
Автор:
kirsten - 2 года назад
-
Ответов:
1 -
Смотреть
-
- запишите продукты уравнения реакции азотной кислоты с серебром HNO3(разб.) + Ag--->HNO3(конц.) + Ag--->даю 30 баллов срочно сор
-
Нужна помощь в задании Exel
-
Предмет:
Информатика -
Автор:
averybaker - 2 года назад
-
Ответов:
1 -
Смотреть
-
