-
Розв'яжіть нерівність: x² + 2x-15 < 0.
-
Предмет:
Алгебра -
Автор:
janessafranco - 3 года назад
-
Ответы 2
-
Ответ:Нерівність x² + 2x - 15 < 0 можна розв'язати, знаходячи корені квадратного трикутника, що відповідає цій нерівності. Для цього знайдемо спочатку точки перетину графіку функції y = x² + 2x - 15 з осіми координат:
x² + 2x - 15 = 0
Застосуємо формулу дискримінанту:
D = b² - 4ac = 2² - 4(1)(-15) = 64
x1,2 = (-2 ± √64) / 2 = -2 ± 4
Отже, x1 = -6 і x2 = 4. Тепер побудуємо табличку знаків функції y = x² + 2x - 15 на інтервалах (-∞, -6), (-6, 4) і (4, +∞):
x -∞ -6 4 +∞
y = x²+2x-15 - - + +
y < 0 + - - +
Таким чином, нерівність x² + 2x - 15 < 0 виконується на інтервалах (-∞, -6) і (3, 4). Розв'язок нерівності можна записати у вигляді:
x ∈ (-∞, -6) ∪ (3, 4)
Объяснение:
-
Автор:
bradynzm6n - 3 года назад
-
7
-
-
Все на фото_________
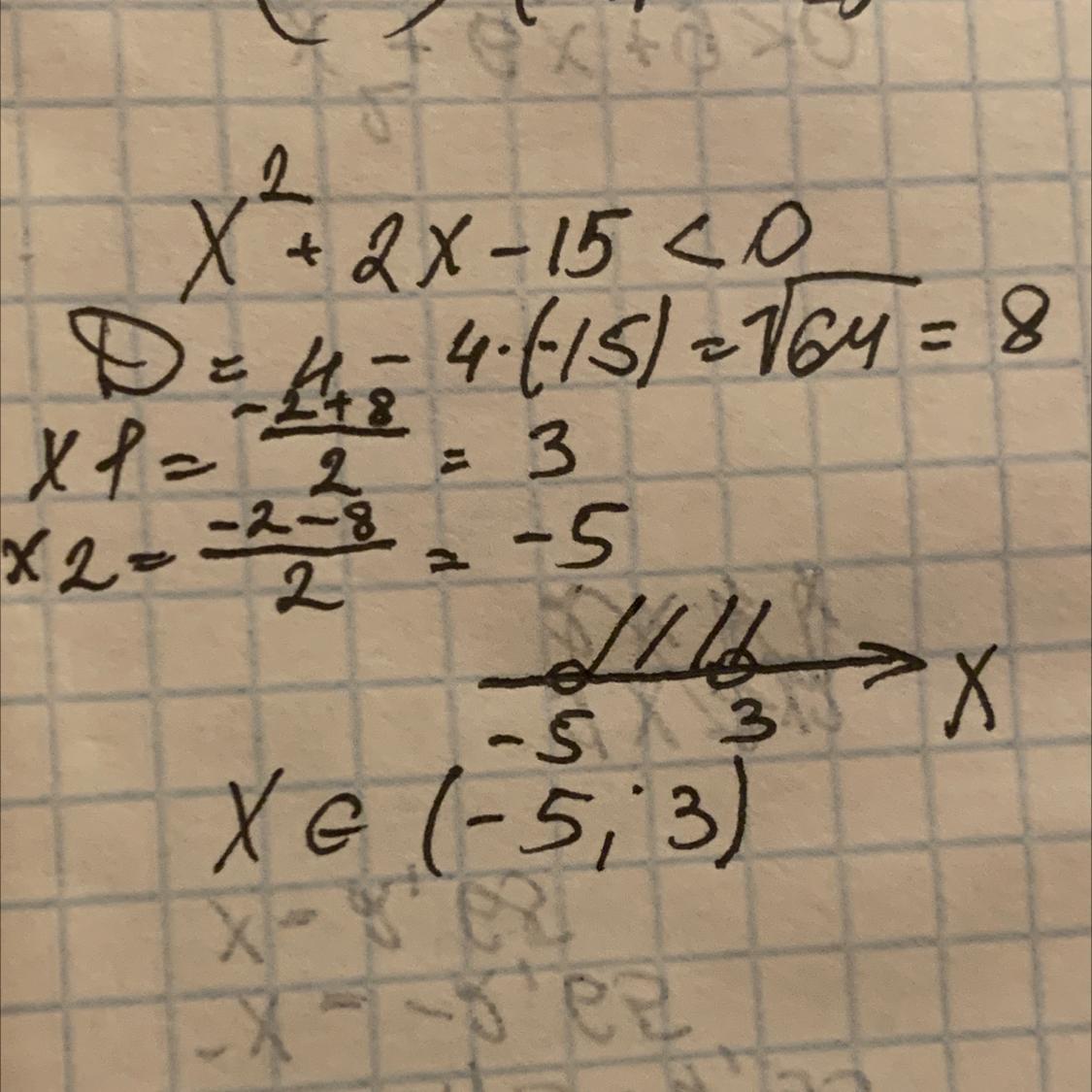
-
Автор:
nathenyzht - 3 года назад
-
8
-
-
Добавить свой ответ
- Виконай віднімання 1)-4,7-5,6; 2)12,5-(-17,3) 3)-2,5-(-9,6) Помогите пожалуста срочно нужно
-
«я не знаю,що він робив вчора ввечері» зробити схему до цього речення
-
Предмет:
Українська мова -
Автор:
mauricio - 3 года назад
-
Ответов:
1 -
Смотреть
-
- Допоможіть будь ласка!!1) Складіть "асоціативний кущ" Михайло Драгоманов.2) Визначте головні напрямки модернізації промисловості та с/г.3) доведіть що громадський рух належав до українофільського етапу національного відродження.
-
2). Мідний дріт довжиною 250 м має опір 0,68 Ом. Якою є площа поперечного перерізу дроту?
-
Предмет:
Физика -
Автор:
milagros80 - 3 года назад
-
Ответов:
1 -
Смотреть
-
