-
умоляю помогите полностью решить пожалуйста дам 50 баллов срочнооо
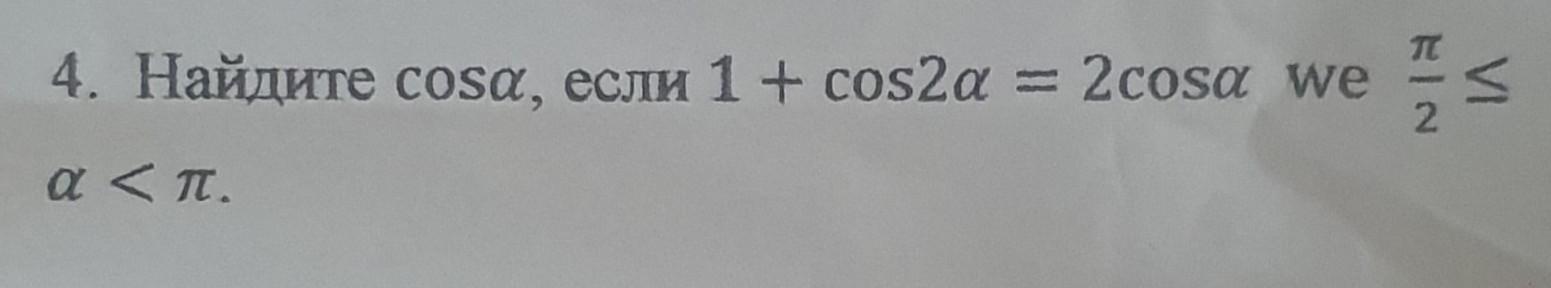
Ответы 1
-
Начнем с исходного уравнения:
1 + cos(2a) = 2cos(a)
Мы можем использовать тригонометрические тождества, чтобы переписать cos(2a) в терминах cos(a):
cos(2a) = 2cos^2(a) - 1
Теперь мы можем заменить cos(2a) на правой стороне уравнения:
1 + 2cos^2(a) - 1 = 2cos(a)
Упрощая, получаем:
2cos^2(a) = 2cos(a)
Делим обе стороны на 2cos(a):
cos(a) = 1
Так как 0 ≤ a < π/2, единственное решение это a = 0.
Таким образом, мы получаем, что a = 0 является единственным решением исходного уравнения, а значит cos(α) = cos(0) = 1.
-
Автор:
emilypage - 2 года назад
-
2
-
-
Добавить свой ответ
Еще вопросы
-
Чи може вірус вивести апаратну частину комп’ютера з ладу?
-
Предмет:
Информатика -
Автор:
arrow - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
За словами Т.Шевченка, свою історію потрібно вивчати:
-
Предмет:
Українська література -
Автор:
nevaehwright - 2 года назад
-
Ответов:
1 -
Смотреть
-
- Геометрия. 9 класс. Помогите, пожалуйста, решить задание
-
Примеры по алгебре
-
Предмет:
Русский язык -
Автор:
syllable - 2 года назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
