-
Допоможіть будь ласка!! :) У геометричній прогресії b1=1/625, q5. Знайти b2
Ответы 2
-
Відповідь:
Пояснення:
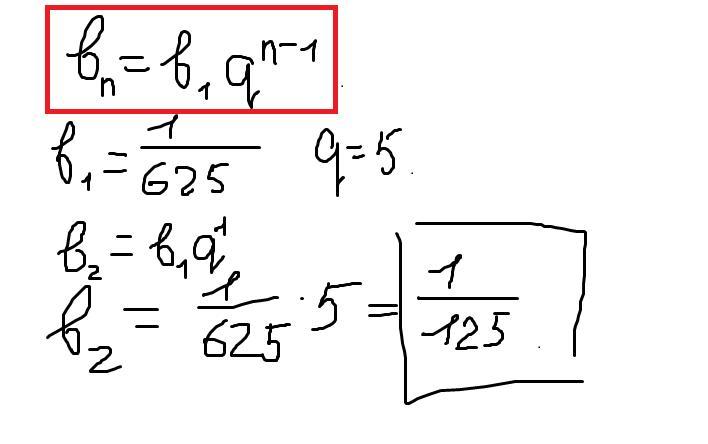
-
Автор:
pashafrost - 2 года назад
-
3
-
-
Вiдповiдь :
b2 = 1/3125.
Щоб знайти b2 у геометричній прогресії з b1 = 1/625 та q^5 = b5, ми можемо використати формулу bn = b1 * q^(n-1). Але нам потрібно знайти q, щоб застосувати цю формулу.
Ми знаємо, що q^5 = b5, тобто q = корінь п'ятої степені з b5. Ми можемо знайти значення b5, використовуючи формулу bn = b1 * q^(n-1) з n = 5:
b5 = b1 * q^(5-1) = b1 * q^4 = (1/625) * q^4.
Тому q^5 = b5 = (1/625) * q^4, що дорівнює q = корінь п'ятої степені з ((1/625) * q^4).
q^4 можна знайти, помноживши обидві сторони цього рівняння на q:
q^5 = (1/625) * q^4
q * q^4 = (1/625) * q^4
q = 1/5
Тому q = 1/5, і ми можемо використовувати формулу bn = b1 * q^(n-1), щоб знайти b2:
b2 = b1 * q^(2-1) = b1 * q = (1/625) * (1/5) = 1/3125.
Отже, b2 = 1/3125.
-
Автор:
tuxmbkv - 2 года назад
-
2
-
-
Добавить свой ответ
- На шовковій нитці висить металева куль- ка масою 20 г, якій надали заряд -20 мкл. Знизу до цієї кульки підносять ще одну негативно заряджену кульку. При відстані 20 см між кульками сила натягу нитки до- Рiвнює 100 мн. Визнач заряд другої куль- ки. Зроби пояснювальний малюнок.
- После путешествия ребята решили сравнить величайшие реки мира. Помогите им заполнить таблицу " Сравнительная характеристика Амазонки и Нила"Помогите пожалуйста доделать, и если не сложно проверьте сделанное
-
Алгебра , умоляю помогите
-
Предмет:
Физика -
Автор:
snowyforbes - 2 года назад
-
Ответов:
3 -
Смотреть
-
-
Химия 11 класс пожалуйста
-
Предмет:
Химия -
Автор:
elwoodfletcher - 2 года назад
-
Ответов:
2 -
Смотреть
-
