Розвязати інтеграл методом заміни зміної або інтегрування частинами. Здати до вівторка (14.03)

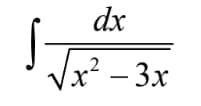
Ответ:

Объяснение:

На рисунке изображено две касающиеся окружности и отрезок, соединяющий их точки касания. Пусть радиус меньшей окружности равен r, а радиус большей окружности равен R.

Так как окружности касаются друг друга, то отрезок, соединяющий их точки касания, является их общей касательной. Из геометрии известно, что касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Поэтому отрезок AB является перпендикуляром к радиусу меньшей окружности, проведенному в точку касания, и к радиусу большей окружности, проведенному в точку касания. Значит, он является высотой треугольника OAC.

Треугольник OAC является прямоугольным, так как один из его углов (угол OAC) равен 90 градусам. Из геометрии известно, что высота, проведенная к гипотенузе прямоугольного треугольника, является средним гармоническим между отрезками гипотенузы, на которые она делит эту гипотенузу. Поэтому имеем:

AB² = OC * OA

AB² = (R - r) * (R + r)

AB = sqrt[(R - r) * (R + r)]

Ответ: AB = sqrt[(R - r) * (R + r)].