упростите вырожкние sin(n-a)*ctg(3n/2-a)/tg(2п-a)cos(n/2+a)

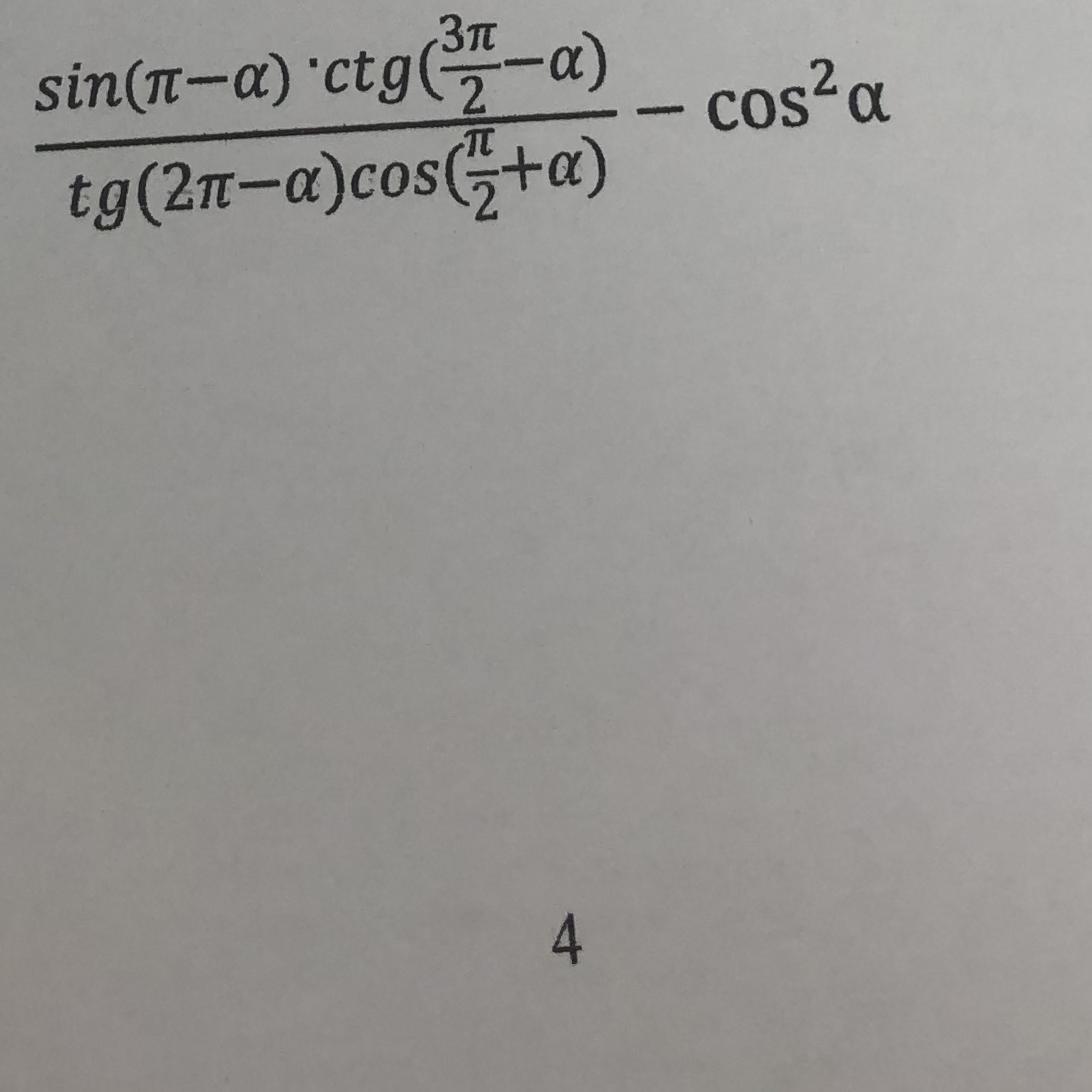
Ответ:

Перепишем выражение, используя определение тангенса, котангенса, и формулы тригонометрии:

sin(n-a) * ctg(3n/2-a) / tg(2π-a) * cos(n/2+a) =

= (sin(n-a) * cos(3n/2-a)) / (sin(2π-a) * sin(a-n)) * cos(n/2+a) / sin(π-a) =

= (-sin(n-a) * cos(n-a)) / (sin(a) * sin(2n-a)) * cos(n/2+a) / cos(a) =

= -(sin(n-a) * cos(n-a) * cos(n/2+a)) / (sin(a) * cos(a) * sin(2n-a)) =

= - (sin(n-a) / sin(2n-a)) * (cos(n-a) * cos(n/2+a) / cos(a))

Замечаем, что второй множитель можно преобразовать:

cos(n-a) * cos(n/2+a) / cos(a) = cos(n/2+a) / cos(a) * cos(a-n) =

= ctg(a) * sin(n-a)

Подставляем это в исходное выражение:

-(sin(n-a) / sin(2n-a)) * (cos(n-a) * cos(n/2+a) / cos(a)) =

= -(sin(n-a) / sin(2n-a)) * [ctg(a) * sin(n-a)] =

= - ctg(a) * (sin(n-a) / sin(2n-a))²

Ответ: выражение можно упростить до формы - ctg(a) * (sin(n-a) / sin(2n-a))².