Знайти суму цілих розв'язків нерівності -2х²+7х-5≥0​

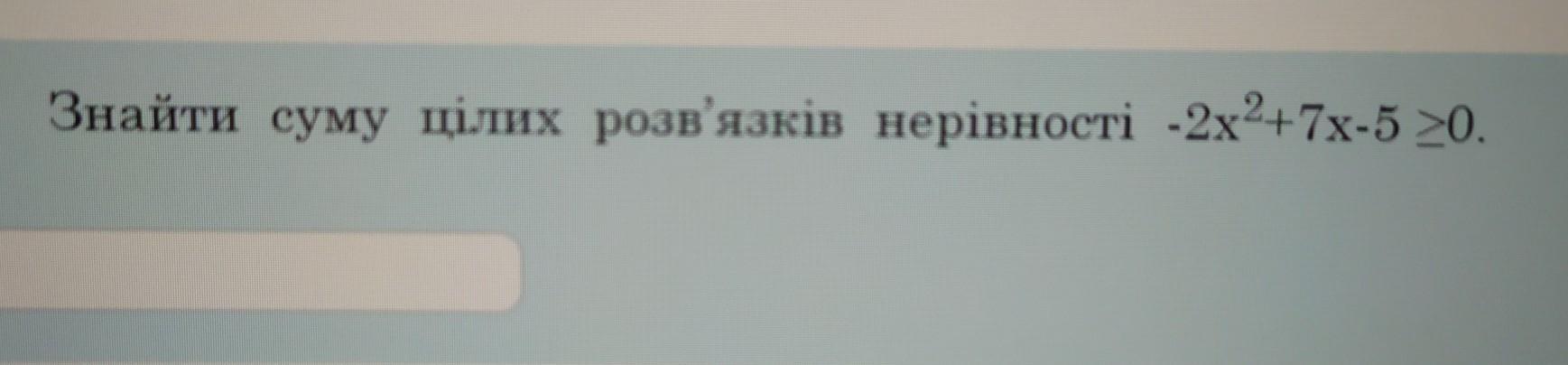
Для знаходження розв'язків даної нерівності потрібно спочатку знайти корені відповідного квадратного рівняння -2х²+7х-5=0. Використовуючи формулу дискримінанту, отримаємо:

D = b² - 4ac = 7² - 4*(-2)*(-5) = 9

Так як дискримінант D > 0, то рівняння має два різних дійсних корені:

x1 = (-b + sqrt(D)) / 2a = (7 + 3) / (-4) = -1

x2 = (-b - sqrt(D)) / 2a = (7 - 3) / (-4) = -1/2

Тепер можна побудувати знакову таблицю і знайти розв'язки нерівності:

-2x^2 + 7x - 5 ≥ 0

x < -1 - + - | 0

x > -1/2 + - + | +

Отже, нерівність -2x^2 + 7x - 5 ≥ 0 виконується при x ≤ -1 або x ≥ 2. Розв'язком є сума цілих чисел у цьому інтервалі:

-1 + 0 + 1 = 0

Таким чином, сума цілих розв'язків нерівності -2x²+7x-5≥0 дорівнює 0.