-
найти площадь фигуры ограниченной астроидой x=a cos(t)^3 y= b sin(3t)^3
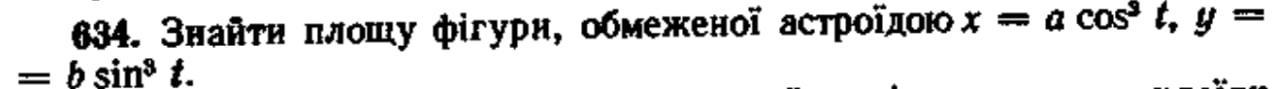
-
Предмет:
Алгебра -
Автор:
marthacallahan - 2 года назад
-
Ответы 1
-
S = ∫[a,b] y dx,
x = a cos(t)^3,
y = b sin(3t)^3,
S = ∫[t1,t2] x dy,
S = ∫[0,2π] a cos(t)^3 * 3b sin(3t)^2 cos(t) dt
S = 3ab∫[0,2π] cos^4(t) sin^2(3t) dt
S = 3ab∫[0,2π] (1-sin^2(t))^2 sin^2(3t) dt
S = 3ab∫[0,2π] (sin^6(t) - 2sin^4(t) + sin^2(t)) sin^2(3t) dt
S = 3ab ( [sin^7(t)/7 - 2sin^5(t)/5 + sin^3(t)/3]sin^3(3t)/9 |0 to 2π )
S = 81abπ/35
-
Автор:
tanglescrwi - 2 года назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Укажите с точностью до десятилетия время, когда в России появился первый сословно-представительный орган·1550·1610·1590·1540
- Помогите я тупой.3. Допишіть продукти реакцій, поставте коефіцієнт НТИ: A. FeCl,+КОН= Б. AgNO,+NaCl ШII рівень
-
3 речення спонукальне питальне розповідне
Підкресліть підмет та присудок
-
Предмет:
Українська мова -
Автор:
destinyevans - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Вірним другом і помічником закоханих у пʼєсі виступає: а) Тібальт; 6) Меркуціо; в) Лоренцо.
-
Предмет:
Литература -
Автор:
gilmore - 2 года назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
