-
Вычислить сумму целочисленных решений неравенств x^2+14z+48/x+5 + x^2-9x+4/z-9 ≥ 2x+9 принадлежащих промежутку [-10;10]
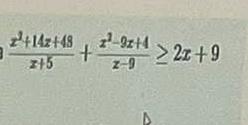
Ответы 1
-
Если сначала искать нули, то получится что-то такое
\dfrac{x^{2}+14\,x+48}{x+5}+\dfrac{x^{2}-9\,x+4}{x-9}\geq 2\,x+9\\\dfrac{\left(x^{2}+14\,x+48\right)\,\left(x-9\right)+\left(x^{2}-9\,x+4\right)\,\left(x+5\right)+\left(-2\,x-9\right)\,\left(x^{2}-4\,x-45\right)}{\left(x-9\right)\,\left(x+5\right)}\geq 0\\\dfrac{7\,x-7}{\left(x-9\right)\,\left(x+5\right)}\geq 0\Leftrightarrow \dfrac{x-1}{\left(x-9\right)\,\left(x+5\right)}\geq 0\Rightarrow \begin{gathered}x\in \left(-5;\,1\right]\cup\left(9;\,\infty\right)\end{gathered}
На фото ниже, я решил избавиться от этих вычислений и поделить числитель на знаменатель, хорошо всё сокращалось, но почему-то не получился ответ
В любом случае первое решение верное и ответ верный!
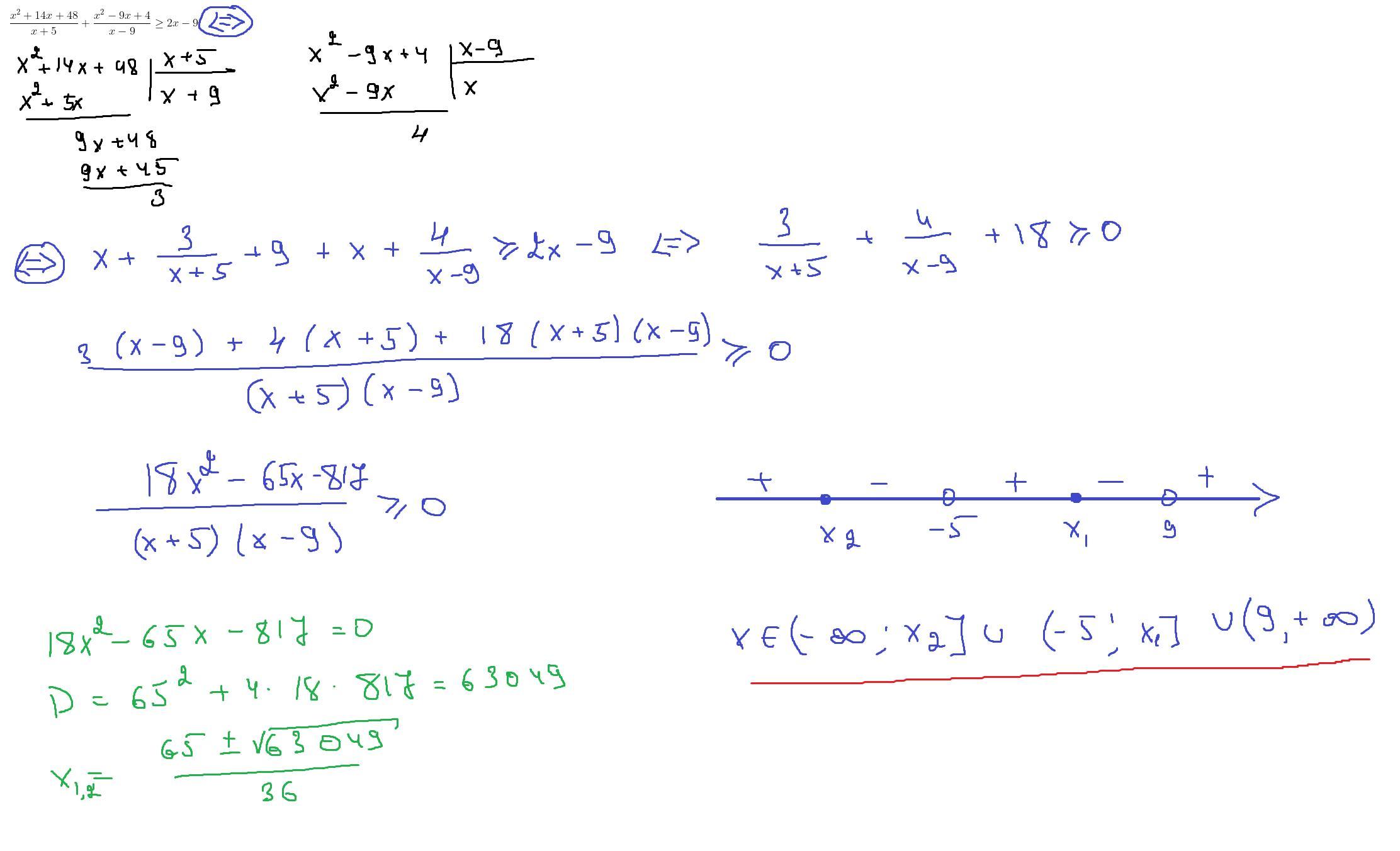
-
Автор:
kiraconley - 2 года назад
-
7
-
-
Добавить свой ответ
-
Пожалуйста, два предложения на украинском со словами повільно, и голосно.
Заранее большое спасибо!!
-
Предмет:
Українська мова -
Автор:
snoopy77 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
homework scool work sometimes предложения
-
Предмет:
Английский язык -
Автор:
brennacampos - 2 года назад
-
Ответов:
1 -
Смотреть
-
- окола шара описана правильная четырехугольная призма объемом 512. найдите радиус шара
-
Напишите НАИМЕНЬШЕЕ число х, для которого ЛОЖНО высказывание: (x>=20) ИЛИ (x нечетный)
-
Предмет:
Информатика -
Автор:
griffen - 2 года назад
-
Ответов:
1 -
Смотреть
-
