-
Здравствуйте, подскажите пожалуйста как решать такие неравенства вида ||f| - |g|| >= |t|
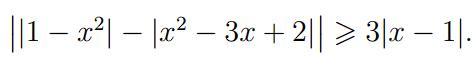
-
Предмет:
Алгебра -
Автор:
valeriadiaz - 2 года назад
-
Ответы 1
-
Чтобы решить неравенства вида ||f| - |g|| >= |t|, можно использовать следующий метод:
Разделите неравенство на два случая: когда |f| - |g| >= 0 и когда |f| - |g| < 0.
В первом случае, ||f| - |g|| = |f| - |g|, так что неравенство превращается в |f| - |g| >= |t|
Во втором случае, ||f| - |g|| = -(|f| - |g|), так что неравенство превращается в - (|f| - |g|) >= |t|
Решите каждый случай отдельно, используя обычные методы решения неравенств.
Объедините решения обоих случаев, чтобы получить окончательное решение.
если у нас есть неравенство ||1 - x^2| - |x^2 - 3x + 2|| >= 3|x - 1|, мы можем разделить его на два случая:
Когда |1 - x^2| - |x^2 - 3x + 2| >= 0, неравенство превращается в |1 - x^2| - |x^2 - 3x + 2| >= 3|x - 1|
Когда |1 - x^2| - |x^2 - 3x + 2| < 0, неравенство превращается в - (|1 - x^2| - |x^2 - 3x + 2)| >= 3|x - 1| Затем мы можем решить каждый случай отдельно и объединить решения, чтобы получить окончательное решение.
-
Автор:
zacharyvtbo - 2 года назад
-
10
-
-
Добавить свой ответ
-
3. На сколько градусов 0,65 развёрнутого угла больше примого угла?
-
Предмет:
Математика -
Автор:
kayleighcarr - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Составить рассказ о домашнем животном на 15 предложений используя конструкции to be, there is, there are, have got,has got, can все конструкции должны быть в тексте составит 10 вопросов с кратким ответом
Используя простые приложения.
Заранее спасибо!
-
Предмет:
Английский язык -
Автор:
lauryn - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Куб площадью 96 см² разрезан на равные кубики со стороной 1 см. Они уложены друг на друга в форме прямоугольного параллелепипеда. Найдите высоту параллелепипеда.
-
Предмет:
Математика -
Автор:
natalietaylor - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Отрезок длиной 20 см разделен на пять равных частей. Найди расстояние
между серединами крайних частей.
Ответ?
-
Предмет:
Математика -
Автор:
coco92 - 2 года назад
-
Ответов:
1 -
Смотреть
-
