Вопрос в фото докажите что...при всех действительных значениях...

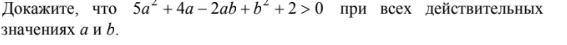
Ответ:

5a^2+4a -2ab + b^2 + 2 > 0\\a^2 - 2ab + b^2 + 4a^2 + 4a + 2 > 0\\(a-b)^2 + 4a^2 + 4a + 1 > -1\\(a-b)^2 + (2a+1)^2 > -1

Сумма квадратов неотрицательна, то есть больше, чем -1. Значит для любых a,b неравенство выполняется.

5a^2+4a-2ab+b^2+2=a^2-2ab+b^2+4a^2+4a+2=(a-b)^2+\\ \\ +4(a+\frac{1}{2})^2+1 > 0

Неравенство верно при любых a и b, поскольку левая часть всегда положительно