(2a/a-7 - 4a/a²-14a+49) : a-9/a²-49 +28a/7-a = 2a довести тотожність​

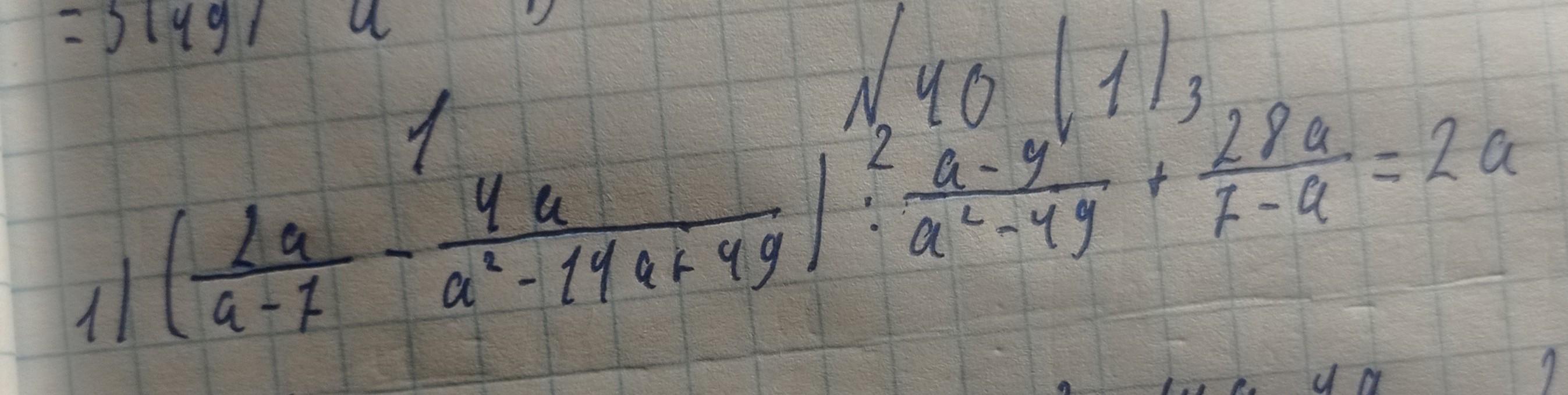
Ответ:

Объяснение:

a^2-14a+49=(a-7)^2 \\a^2-49=(a-7)*(a+7)\\\frac{28a}{7-a}= - \frac{28a}{a-7}

= > (\frac{2a}{a-7} -\frac{4a}{a^2-14a+49} ): \frac{a-9}{a^2-49} +\frac{28a}{7-a} =\\\\=(\frac{2a}{a-7}-\frac{4a}{(a-7)^2})*\frac{(a-7)(a+7)}{a-9}-\frac{28a}{a-7} = \\ \\=(\frac{2a*(a-7)-4a}{(a-7)^2}* \frac{(a-7)(a+7)}{a-9}-\frac{28a}{a-7} =\\\\=\frac{(2a^2-14a-4a)*(a+7)}{(a-7)*(a-9)} -\frac{28a}{a-7}= \frac{(2a^2-18a)(a+7)}{(a-7)(a-9)} -\frac{28a}{a-7}=

= \frac{2a(a-9)(a+7)}{(a-7)(a-9)}-\frac{28a}{a-7} =\frac{2a(a+7)}{a-7}-\frac{28a}{a-7}=\\ \\ =\frac{2a^2+14a-28a}{a-7} =\frac{2a^2-14a}{a-7}= \frac{2a(a-7)}{a-7}=2a

2a=2a что и требовалось доказать !