-
Срочно !!! Корень 2 sinx+1=0
-
Предмет:
Алгебра -
Автор:
immanuelwaller - 2 года назад
-
Ответы 2
-
2 sinx+1=0
Вычитаем 1 с обеих сторон уравнения
\(\sqrt{2} \sin(x) = -1\)
Делим обе стороны на \sqrt{2}
\(\sin(x) = -\frac{1}{\sqrt{2}}\)
Этот угол в тригонометрической системе координат находится в III квадранте, где значение синуса отрицательно. Одно из углов, у которого синус равен\(-\frac{1}{\sqrt{2}}\), это \(x = -\frac{\pi}{4}\) (или\(-45^\circ\)).
Но по мимо этого угла, синус функция периодична с периодом \(2\pi\), поэтому можно добавить к \(-\frac{\pi}{4}\) любое кратное \(2\pi\) значение, чтобы получить другие решения:
\[x = -\frac{\pi}{4} + 2\pi n, \quad n \in \mathbb{Z}\].
\(\sqrt{2} \sin(x) + 1 = 0\)
это:
\[x = -\frac{\pi}{4} + 2\pi n, \quad n \in \mathbb{Z}\].
-
Автор:
durán0mqu - 2 года назад
-
0
-
-
####################
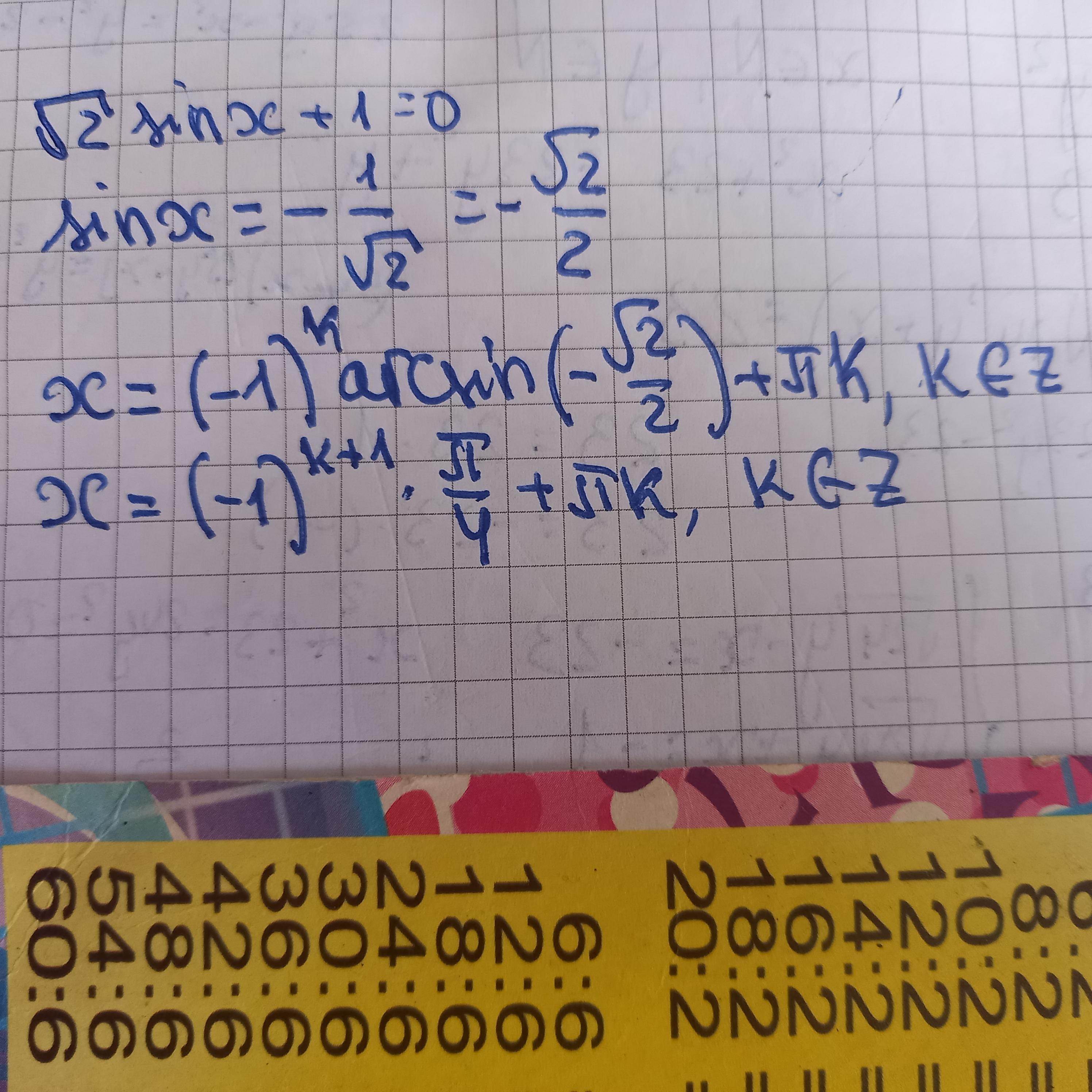
-
Автор:
conner298 - 2 года назад
-
0
-
-
Добавить свой ответ
-
3 Match the definitions with the words below. There are two extra words. charger hall helmet jumper mushroom nephew niece pole vault 1 You use this when your battery is low. 20 When the sun goes down at the end of the day. 21 This isn't meat or fruit - but it is good for you. 22 This protects your head.. 23 An athletic sport where you have to get over a high bar.. 24 Warm top for the winter. 25 Your brother's daughter.. 26 The low area between two mountains. 27 The room inside the entrance of a house or apartment. sunrise sunset valley СРОЧНО!!!!! ПОМОГИТЕ даю 100 баллов
-
Предмет:
Английский язык -
Автор:
maciehodges - 2 года назад
-
Ответов:
2 -
Смотреть
-
-
please help urgently needed помогите пожалуйста ) срочно нужно
-
Предмет:
Английский язык -
Автор:
coralie1 - 2 года назад
-
Ответов:
2 -
Смотреть
-
-
Коротка розповідь повісті Андрія Чайковського "за сестрою"
-
Предмет:
Литература -
Автор:
kayleigh - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
19. Решите уравнения: a) 14x + 18x = 320; b) 21y - 4y + 6y = 69; c) 11x + 3x = 28; d) 16y - 4y +8y = 100.d)16y-4y+8y пж даю 30 баллов
-
Предмет:
Математика -
Автор:
aedanbender - 2 года назад
-
Ответов:
1 -
Смотреть
-
