-
Как это упростить, зная что, а - просто произвольное число, х намного больше a ?
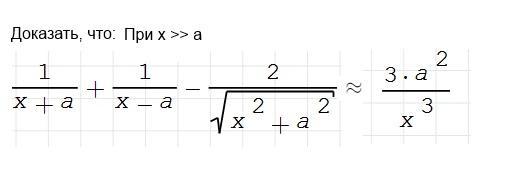
Ответы 1
-
первые две функции разложить в ряд Тейлора до квадратов
\displaystyle\frac{1}{x+a} = \frac{1}{x}\frac{1}{1+a/x}\approx\frac{1}{x}(1-a/x+(a/x)^2) = \frac{1}{x}-\frac{a}{x^2}+\frac{a^2}{x^3}\\\\\frac{1}{x-a} = \frac{1}{x}\frac{1}{1-a/x}\approx\frac{1}{x}(1+a/x+(a/x)^2) = \frac{1}{x}+\frac{a}{x^2}+\frac{a^2}{x^3}
Для третьей функции хватит и линейного разложения
\displaystyle \frac{1}{\sqrt{x^2+a^2}} = \frac{1}{x}(1+a^2/x^2)^{-1/2}\approx\frac{1}{x}(1-a^2/(2x^2)) = \frac{1}{x}-\frac{a^2}{2x^3}
Сложим все три выражения, не забыв умножить последнее на -2
много чего уйдет и останется
\displaystyle\frac{3a^2}{x^3}
-
Автор:
kobejnkk - 2 года назад
-
4
-
-
Добавить свой ответ
-
0,8 •(2y +3) - 1,2 • (3y - 4) = 0,6,
-
Предмет:
Математика -
Автор:
parker78 - 2 года назад
-
Ответов:
2 -
Смотреть
-
-
помогите пожалуйста срочно я не понимаю как это делать
-
Предмет:
Немецкий язык -
Автор:
lola76 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Туристы сначала прошли 40% всего пути, а потом 30% остатка. Сколько процентов всего пути осталось пройти?
-
Предмет:
Математика -
Автор:
gideon - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
В шар массы М, лежащий на кольце, попадает пуля массы т, и пробивает его. Скорость пули
v была направлена вертикально вверх вдоль прямой, проходящей через центр шара. На какую высоту над кольцом подпрыгнет шар, если пуля после пробивания шара поднялась на высоту Н?
-
Предмет:
Физика -
Автор:
marleneroy - 2 года назад
-
Ответов:
1 -
Смотреть
-
