-
Решите это уравнение развернуто. Буду очень благодарен (4)/((x+1)^(2))+(2)/(1-x^(2))-(1)/(1-x)=0
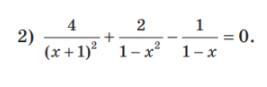
Ответы 1
-
(4)/((x+1)^(2)) + (2)/(1-x^(2)) - (1)/(1-x) = 0
Сначала умножим обе стороны уравнения на общий знаменатель, который равен (x+1)^(2)(1-x)(1-x).
4(1-x) + 2(x+1)^(2) - (1)(x+1)^(2)(1-x) = 0
Теперь раскроем скобки и упростим уравнение:
4 - 4x + 2(x^(2) + 2x + 1) - (x^(2) + 2x + 1)(1-x) = 0
Раскрываем скобки:
4 - 4x + 2x^(2) + 4x + 2 - x^(3) - 3x^(2) - x + 2 = 0
Сгруппируем по степеням x:
x^(3) - 3x^(2) + 2x^(2) - x + 4x - 4 + 2 = 0
x^(3) - x^(2) - x - 2 = 0
Теперь у нас есть кубическое уравнение. Его решение можно найти аналитически, используя методы алгебры или численные методы. Если вы хотите численное решение, то могу помочь с этим.
-
Автор:
babe1swc - 2 года назад
-
8
-
-
Добавить свой ответ
Еще вопросы
- Покажите на карте 7 стран лишенных к выходу к морю
-
Нужно определить абсолютную относительную и приведенную погрешности вольт метра
-
Предмет:
Физика -
Автор:
taniyahbeltran - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
73×605-19×760-501×(3041-2988)=
-
Предмет:
Математика -
Автор:
benjamin - 2 года назад
-
Ответов:
1 -
Смотреть
-
- 8. Найдите углы параллелограмма, если сумма двух из них равна: а) 80 б) 100; в) 160°.
How much to ban the user?
1 hour
1 day
100 years
