-
A Преобразуйте произведение в сумму (58—60): 58, a) sin 32º . sin 10; б) sin 45° . sin 15°; в) cos 56º. cos 16°; cos 48°. cos 24. 59. a) sin B) COS П 24 П 5 sin 7 П ; 24' П ва COS 6) cos T 10 г) sin - TC 10 . sin COS T 8°
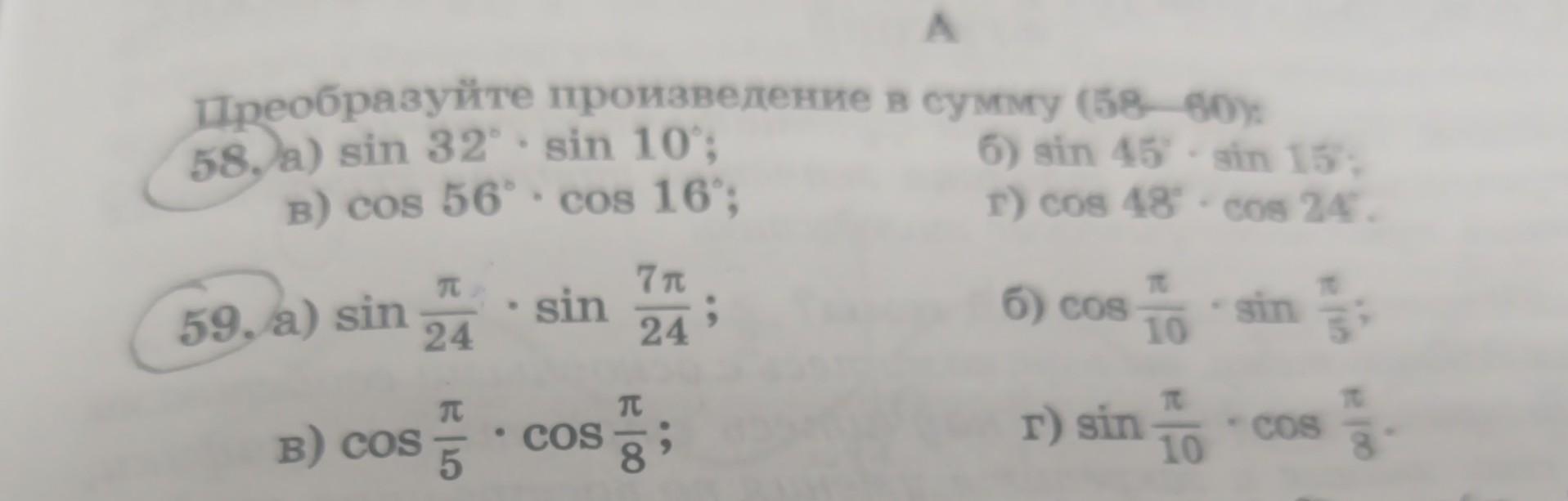
-
Предмет:
Алгебра -
Автор:
gummi bear - 2 года назад
-
Ответы 1
-
Ответ:
Для преобразования произведения тригонометричных функций в сумму, вы можете использовать тригонометрические формулы для синуса и косинуса. Вот как это можно сделать:
а) \(sin(32°) * sin(10°)\):
Используем формулу для синуса произведения двух углов:
\[sin(A) * sin(B) = \frac{1}{2} * [cos(A - B) - cos(A + B)]\]
Подставим значения:
\[sin(32°) * sin(10°) = \frac{1}{2} * [cos(32° - 10°) - cos(32° + 10°)]\]
\[= \frac{1}{2} * [cos(22°) - cos(42°)]\]
б) \(sin(45°) * sin(15°)\):
Используем ту же формулу:
\[sin(45°) * sin(15°) = \frac{1}{2} * [cos(45° - 15°) - cos(45° + 15°)]\]
\[= \frac{1}{2} * [cos(30°) - cos(60°)]\]
в) \(cos(56°) * cos(16°)\):
Используем формулу для косинуса произведения двух углов:
\[cos(A) * cos(B) = \frac{1}{2} * [cos(A - B) + cos(A + B)]\]
Подставим значения:
\[cos(56°) * cos(16°) = \frac{1}{2} * [cos(56° - 16°) + cos(56° + 16°)]\]
\[= \frac{1}{2} * [cos(40°) + cos(72°)]\]
г) \(cos(48°) * cos(24°)\):
Та же формула для косинуса:
\[cos(48°) * cos(24°) = \frac{1}{2} * [cos(48° - 24°) + cos(48° + 24°)]\]
\[= \frac{1}{2} * [cos(24°) + cos(72°)]\]
Теперь вы можете вычислить числовые значения для каждого выражения, используя значения косинуса и синуса для соответствующих углов.
-
Автор:
oto50k4 - 2 года назад
-
1
-
-
Добавить свой ответ
-
Старинный отопительный прибор в виде ямы
-
Предмет:
Окружающий мир -
Автор:
gordon51 - 2 года назад
-
Ответов:
2 -
Смотреть
-
- 7 Кто признал титул Барсбека ынанчы а) Танская империя 7 Алп Бильге каган? б) Тюргешский каганат в) Восточный Тюркский каганат
-
Прочитайте названия произведений и определите их жанр.
«Происхождение мира и богов»
«Похищение Европы»
Ответ запишите в Им.п, ед.ч, без кавычек и дополнительных знаков в конце. Например, легенда.
-
Предмет:
Литература -
Автор:
nehemiah - 2 года назад
-
Ответов:
1 -
Смотреть
-
- Имеют ли единицы измерения углов "минута" (1/60°) и "секунда" (1/360°) отношение к одноименным единицам времени?
