-
Помогите найти предел срочно, ясно и понятно. Не знаю как решать.
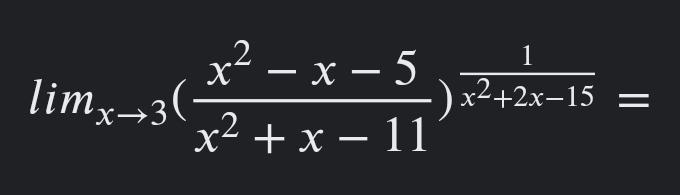
Ответы 1
-
OTBET: \displaystyle\ lim_{n \to 3}(\frac{x^2-x-5}{x^2+x-11})^\frac{1}{x^2+2x-15} =1.
Объяснение:
\displaystyle\\ \lim_{n \to 3}(\frac{x^2-x-5}{x^2+x-11})^\frac{1}{x^2+2x-15} .
Подставляем значение х=3 в формулу:
\displaystyle\\(\frac{3^2-3-5}{3^2+3-11} )^\frac{1}{3^2+2*3-15} =(\frac{9-3-5}{9+3-11} )^\frac{1}{9+6-15} =(\frac{1}{1} )^\frac{1}{0} =1^\infty=1.
-
Автор:
ashtynriddle - 2 года назад
-
5
-
-
Добавить свой ответ
Еще вопросы
-
Будет ли плевать на всё если не высплюсь
-
Предмет:
Другие предметы -
Автор:
wiz - 2 года назад
-
Ответов:
5 -
Смотреть
-
-
составить кластер к слову профессия пж могите!!! дам 50
-
Предмет:
Русский язык -
Автор:
tony19 - 2 года назад
-
Ответов:
1 -
Смотреть
-
- ОЧЕНЬ ЛЕГКИЙ ВОПРОСКрапками позначено положення тіла через однакові інтервали часу.Виберіть рисунок, що зображує рівномірний рух тіла з більшою швидкістю
- Бжб 2 тоқсан биология 7 сынып даю 100 балл
How much to ban the user?
1 hour
1 day
100 years
