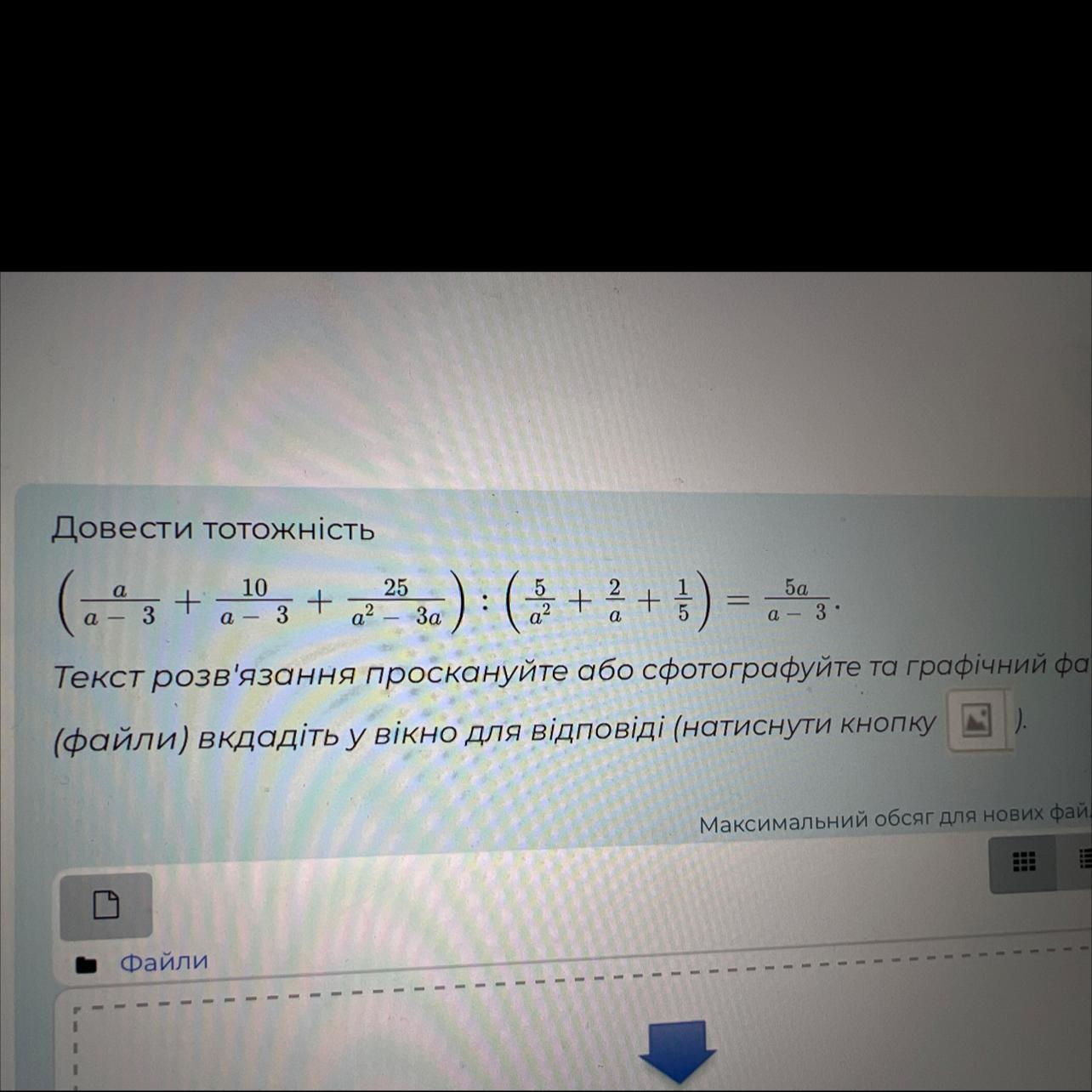
СРОЧНО АЛГЕБРА СДАВАТЬ ЧЕРЕЗ 10 МИНУТ!!!! Довести тотожність 10 (a-3 +²²3 +2² 2²5 30) : (5 + ² + ²) = 53. 5a a- За 5 a -

Ответ:

Объяснение:

Давайте розглянемо вираз та спростимо його:

\[

\frac{{(a-3 + 2^{23} + 2^{25} + 30)}}{{(5 + 2 + 2)}} = 53 \cdot \frac{1}{5a}

\]

Після спрощення маємо:

\[

\frac{{(a-3 + 2^{23} + 2^{25} + 30)}}{{9}} = \frac{{53}}{{5a}}

\]

Тепер, помножимо обидві сторони на \(9 \cdot 5a\):

\[

9 \cdot 5a \cdot \frac{{(a-3 + 2^{23} + 2^{25} + 30)}}{{9}} = 9 \cdot 5a \cdot \frac{{53}}{{5a}}

\]

Спростимо:

\[

5 \cdot (a-3 + 2^{23} + 2^{25} + 30) = 53 \cdot 9

\]

\[

5a - 15 + 5 \cdot 2^{23} + 5 \cdot 2^{25} + 150 = 477

\]

Зібравши подібні терміни та спростивши, отримаємо:

\[

5a + 5 \cdot 2^{23} + 5 \cdot 2^{25} = 342

\]

Це є розв'язком вашої тотожності.